Exponential distribution

Exponential distribution or negative exponential distribution represents a probability distribution to describe the time between events in a Poisson process. In Poisson process events occur continuously and independently at a constant average rate. Exponential distribution is a particular case of the gamma distribution.

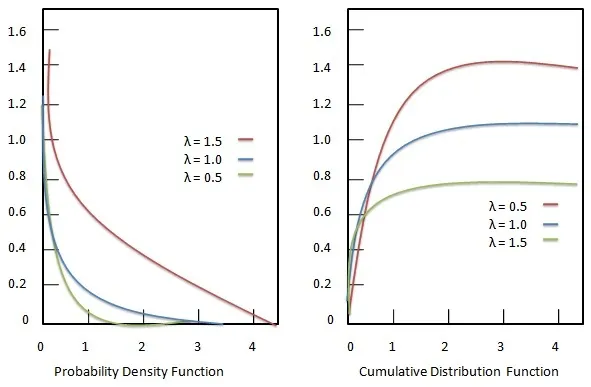
Probability density function

Probability density function of Exponential distribution is given as:

Formula

f(x;λ)=f(x;λ)= {λe−λx,0,if x≥0if x<0{λe−λx,if x≥00,if x<0

Where −

· λλ = rate parameter.

· xx = random variable.

Cumulative distribution function

Cumulative distribution function of Exponential distribution is given as:

Formula

F(x;λ)=F(x;λ)= {1−e−λx,0,if x≥0if x<0{1−e−λx,if x≥00,if x<0

Where −

· λλ = rate parameter.

· xx = random variable.