Circular Permutation

Circular permutation is the total number of ways in which n distinct objects can be arranged around a fix circle. It is of two types.

1. Case 1: - Clockwise and Anticlockwise orders are different.

2. Case 2: - Clockwise and Anticlockwise orders are same.

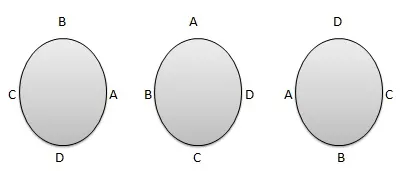
Case 1: Formula

Pn=(n−1)!Pn=(n−1)!

Where −

· PnPn = represents circular permutation

· nn = Number of objects

Case 2: Formula

Pn=n−1!2!Pn=n−1!2!

Where −

· PnPn = represents circular permutation

· nn = Number of objects

Example

Problem Statement:

Calculate circular permulation of 4 persons sitting around a round table considering i) Clockwise and Anticlockwise orders as different and ii) Clockwise and Anticlockwise orders as same.

Solution:

In Case 1, n = 4, Using formula

Pn=(n−1)!Pn=(n−1)!

Apply the formula

P4=(4−1)! =3! =6P4=(4−1)! =3! =6

In Case 2, n = 4, Using formula

Pn=n−1!2!Pn=n−1!2!

Apply the formula

P4=n−1!2! =4−1!2! =3!2! =62 =3