An Odyssey to Discover Round and Squared Pizzas!

The Geometry of a pizza

Hi, everyone. Today we’re going to speak about pizza!

Yes, I’m not crazy! I perfectly know it’s a blog on maths!

Indeed, we want to talk of geometry of pizza and why there are some people who prepare it round and some who prepare it squared…who is earning money from this?

But the real answer I want you to propone today is: do you prefer a round or a squared pizza?

I imagine that the average reaction is another question: “What’s the difference? It’s pizza!”

The difference is huge and I’ll show what it is. Have fun!

Dido and oxhide

There are plenty of mathematical problems called maximum/minimum problems. In general they can be solved in many ways but I have no intentions of explaining the general theory. Some of you probably knew about it from school or at University. To people who reads it for the first time: “don’t be scared!”

In a few words, we try to understand how to minimize or maximize quantities under certain circumstances. An example from history: once upon a time there was Dido, Tyre’s queen, arrived in North Africa at the court of King Iarbas as a refugee. Iarbas decided to give her as much and as could be encompassed by an oxhide. Apart from the strange offering, Dido made lots of strips from the oxhide and made a very tiny rope. Finally, she used it to cover an huge land, the land in which Cartago was founded. Now, the question is: what’s the best geometrical form, having a rope, to obtain the maximum area?

In this example, the question is equivalent to: having fixed the perimeter, what’s the figure with maximum area? The answer is: the circle!

Another example: in an opposite way, fixing the area, what is the figure with smaller perimeter? The answer is: the circle again!

Do you know how to show this fact? To simplify the problem let us consider regular polygons, that are polygons with equal edges. It is possible to show that, fixed area A, the perimeter of a regular n-gon is: <<formula>>

So, this is a very well known formula, don’t you know it? 

We see that the perimeter decreases as n increases, so we could say that the minimum perimeter is when there are an infinite number of edges…so? The circle!

If you compute the limit as n goes to infinity, you get <<formula>> and it’s the perimeter of a circle of area A!

So, we answered the question!

What a Pizza!

Come back to Pizza! We discovered that, fixed area, a round pizza has less perimeter than any other shape. But…perimeter is a thing, border is another. The border is an area, not a line!!

So, now the real question is? Who has the minimal border? Who maximal?

Let us start writing some formulas. A is the fixed area, n is the number of the edges of the regular polygon. Let b be the measure of the border.

The n-gon can be decomposed in n isosceles triangles. The angle in front of the base is 2πn2πn and the area of this triangle is A,=a22sin(2πn)A,=a22sin⁡(2πn), where aa is the apothem. Knowing that A=nA,A=nA,, we have that A=na22sin(2πn)A=na22sin⁡(2πn) and so a=2Ansin(2πn)−−−−−−−√a=2Ansin⁡(2πn).

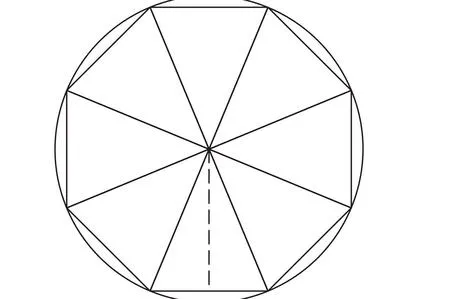
If the pizza was a circle of area AA, then A=πr2A=πr2 where rr is the radius. Hence r=Aπ−−√r=Aπ. Comparing rr and aa we get a=2πnsin(2πn)−−−−−−−√ra=2πnsin⁡(2πn)r. That’s the relation between a and r.

Now, either to the n-gon and to the circle, we cut a border thick bb.  We avoid to make all computations, the final formula for the internal areas of the little triangles are A,int=tan(πn)(πntan(πn)−−−−−−√−b)2Aint,=tan⁡(πn)(πntan⁡(πn)−b)2. So we get: APint=nA,int=ntan(πn)(πntan(πn)−−−−−−√−b)2AintP=nAint,=ntan⁡(πn)(πntan⁡(πn)−b)2.

For the circle, the situation is similar: ACint=π(r−b)2AintC=π(r−b)2.We compare now the two areas computing: ACint?APintAintC?AintP. Using the relation between r and a, we get that the difference is positive if bb has a value between 0 and 2(πntan(πn)√)ntan(πn)−πr2(πntan⁡(πn))ntan⁡(πn)−πr. The value 2(πntan(πn)√)ntan(πn)−π2(πntan⁡(πn))ntan⁡(πn)−π, if n≥3n≥3, is greater than 0.87490.8749 and, as n goes to infinity, it goes to 11.

This means that if b is less than the 87% of the radius, then the internal area of the circle is greater that the n-gon’s one, for all n≥3n≥3. The converse holds for borders!

So, the question “do you prefer a round or a squared pizza? ” has now an answer. Since the square is a 4-gon the answer is: if you like borders, choose a squared pizza, otherwise a round one!

Conclusion (of the average man)

With all those letters, we lost the gist. Let us fix some values.

An average pizza has an area of A=1000cm2A=1000cm2. It turns out that, if the border is between 0 and 17 centimeters, the internal area of the square is smaller than the circle’s one. Since the border is 1 or 2 cm thick, than our result holds!

If you’re not crazy/deviated/maniac/sociopathic/my-cousin/curious, it’s enough for today. See you next time! 

Conclusion (of an applied mathematician, of a economist, of a financial man and similar)

There are other questions: if a pizza company makes round pizzas, how much money does it lose?

Indeed, having a greater area to cover with ingredients, it should spend more.

I made some computations: fixing A=1000cm2A=1000cm2 and b=1cmb=1cm, the internal area of a squared pizza is 877,5cm2877,5cm2 and of a round pizza is 891cm2891cm2. So a squared pizza has 1.5% less ingredients than a round one.

Simplifying, the pizza company would save the 1.5% of the price of ingredients making squared pizzas instead of round pizzas. This means that, if making 100 pizzas costs 400 euros (100 euros for bases and 300 euros for ingredients), supposing that he sells pizzas at a price of 6 euros, he would earn 600-400=200 euros.

Leaving the price to 6 euros, but making squared pizzas, he would save the 1.5% of the costs of ingredients. Hence he would save 4.50 euros. It’s not too much, but it’s only 100 pizzas! Do you want to save more? Make bigger pizzas!

Conclusion (of a pure mathematician)

What? Have I used numbers?

Conclusive conclusion

Well, this is the end! Sayonara!