Computations in Uniform Flow

We can use Manning's formula for discharge to calculate steady uniform flow. Two calculations are usually performed to solve uniform flow problems.

1. Discharge from a given depth

2. Depth for a given discharge

In steady uniform flow the flow depth is know as normal depth.

As we have already mentioned, and by definition, uniform flow can only occur in channels of constant cross-section (prismatic channels) so natural channel can be excluded. However we will need to use Manning's equation for gradually varied flow in natural channels - so application to natural/irregular channels will often be required.

Uniform flow Problem 1 - Discharge from depth in a trapezoidal channel

A concrete lined trapezoidal channel with uniform flow has a normal depth is 2m. The base width is 5m and the side slopes are equal at 1:2

Manning's n can be taken as 0.015 and the bed slope S? = 0.001

What are: a) Discharge (Q) b) Mean velocity (V) c) Reynolds number (Re) Calculate the section properties

This is very large - i.e. well into the turbulent zone - the application of the Manning's equation was therefore valid.

What solution would we have obtained if we had used the Colebrook-White equation?

Probably very similar as we are well into the rough-turbulent zone where both equations are truly applicable.

To experiment an equivalent   k s  value can be calculated for the discharge calculated from  n = 0.015 and y = 2m [ ks = 2.225mm  ]  (Use the  Colebrook-White equation and  the Darcy- Wiesbach equation of open channels -        both given earlier). Then a range of  depths can be chosen and the discharges calculated for these     n and ks   values. Comparing these  discharge calculations will give some idea of the relative differences - they will be very similar.

Uniform flow Problem 2 - Depth from Discharge in a trapezoidal channel

Using the same channel as above, if the discharge is know to be 30m³ /s in uniform flow, what is the normal depth?

Again use equation

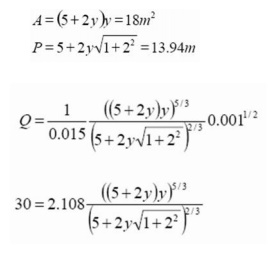
We need to calculate y from this equation.

Even for this quite simple geometry the equation we need to solve for normal depth is complex. One simple strategy to solve this is to select some appropriate values of y and calculate the right hand side of this equation and compare it to Q (=30) in the left. When it equals Q we have the correct y .

Even though there will be several solutions to this equation, this strategy generally works because we have a good idea of what the depth should be (e.g. it will always be positive and often in the

range of 0.5-10 m). In this case from the previous example we know that at Q = 45 m³ /s, y = 2m . So at Q = 30 m³ /s then y < 2.0m.

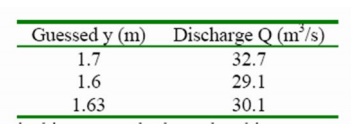
We might also use the bisector method to solve this.

Uniform flow Problem 3 - A compound channel

If the channel in the above example were to be designed for flooding it may have a section like this:

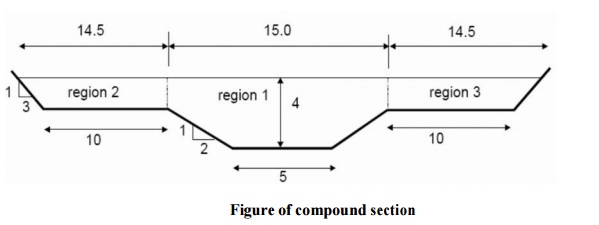
When the flow goes over the top of the trapezoidal channel it moves to the "flood plains" so the section allows for a lot more discharge to be carried.

If the flood channels are 10m wide and have side slopes of 1:3, and the Manning  n           on   these banks is0.035, what are a) the discharge for a flood level of 4m b) the enery coefficient a.          

First split the section as shown in to three regions (this is arbitrary - left to the engineers judgement). Then apply Manning's formula for each section to give three discharge values and the total discharge will be Q = Q1 + Q2 + Q 3 .

Calculate the properties of each region:

This is a  very high  value of a and a clear case of where a velocity coefficient should be used.

Not that this method doe not give completely accurate relationship between stage and discharge because some of the assumptions are not accurate. E.g. the arbitrarily splitting in to regions of fixed Manning n is probably not what is occurring in the actual channel. However it will give an acceptable estimate as long as care is taken in choosing these regions.