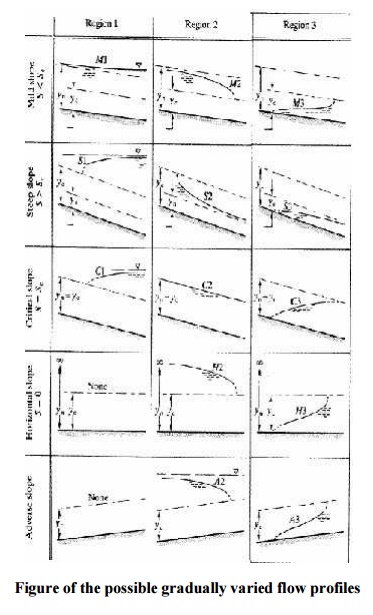
Profile Classifications

Profile Classifications

 Before attempting to solve the gradually varied flow equation a great deal of insight into the type of solutions and profiles possible can be gained by taking some time to examine the equation.

Time spent over this is almost compulsory if you are to understand steady flow in open channels. For a given discharge, S f and Fr²   are functions of depth.

From these inequalities we can see how the sign of dy/dx i.e. the surface slope changes for different slopes and Froude numbers.

Taking the example of a mild slope, shown in the figure below:

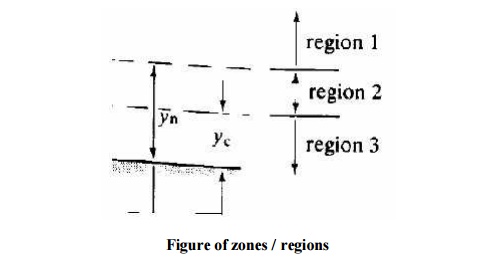
The normal and critical depths are shown (as it is mild normal depth is greater than critical depth). Treating the flow as to be in three zones:

i.   zone 1, above the normal depth

zone 2, between normal and critical depth iii. zone 3, below critical depth The direction of the surface inclination may thus be determined.

The condition at the boundary of the gradually varied flow may also be determined in a similar manner:

zone 1

As y   Q then S f  and Fr   0 and dy/dx   S o

Hence the water surface is asymptotic to a horizontal line for it maximum

As y   y n  then S f  S o and dy/dx 0

Hence the water surface is asymptotic to the line y = y n i.e. uniform flow.

zone 2

As for zone 1 as y approached the normal depth: As  y         y n  then S f  S   o   and

dy/dx  0

Hence the water surface is asymptotic to the line y = y n

But a problem occurs when y approaches the critical depth: As y   y c  then Fr   1 and dy/dx          8

This is physically impossible but may be explained by the pointing out that in this region the gradually varied flow equation is not applicable because at this point the fluid is in the rapidly varied flow regime.

In reality a very steep surface will occur.

zone 3

As for zone 2 a problem occurs when y approaches the critical depth: As yy  c then

Fr      1 and dy/dx   8

Again we have the same physical impossibility with the same explanation. And again in reality a very steep surface will occur.

As y   0 then dy/dx  S o  the slope of bed of the channel !

The gradually varied flow equation is not valid here but it is clear what occurs.

In general, normal depth is approached asymptotically and critical depth at right angles to the channel bed.

The possible surface profiles within each zone can be drawn from the above considerations. These are shown for the mild sloped channel below.

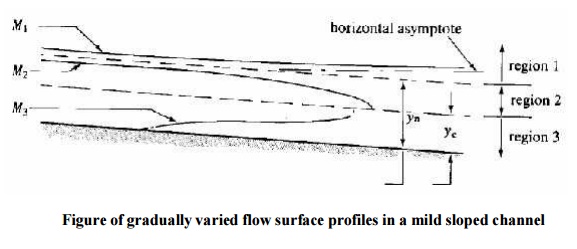
The surface profile in zone 1 of a mild slope is called an M1 curve, in zone 2 an M2 curve and in zone 3 an M3 curve.

All the possible surface profiles for all possible slopes of channel (there are 15 possibilities) are shown in the figure.