Fracture mechanics

Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.

In modern materials science, fracture mechanics is an important tool used to improve the performance of mechanical components. It applies the physics of stress and strain behavior of materials, in particular the theories of elasticity and plasticity, to the microscopic crystallographic defects found in real materials in order to predict the macroscopic mechanical behavior of those bodies. Fractography is widely used with fracture mechanics to understand the causes of failures and also verify the theoretical failure predictions with real life failures. The prediction of crack growth is at the heart of the damage tolerance mechanical design discipline.

There are three ways of applying a force to enable a crack to propagate:

· Mode I fracture – Opening mode (a tensile stress normal to the plane of the crack),

· Mode II fracture – Sliding mode (a shear stress acting parallel to the plane of the crack and perpendicular to the crack front), and

· Mode III fracture – Tearing mode (a shear stress acting parallel to the plane of the crack and parallel to the crack front).

Motivation

The processes of material manufacture, processing, machining, and forming may introduce flaws in a finished mechanical component. Arising from the manufacturing process, interior and surface flaws are found in all metal structures. Not all such flaws are unstable under service conditions. Fracture mechanics is the analysis of flaws to discover those that are safe (that is, do not grow) and those that are liable to propagate as cracks and so cause failure of the flawed structure. Despite these inherent flaws, it is possible to achieve through damage tolerance analysis the safe operation of a structure. Fracture mechanics as a subject for critical study has barely been around for a century and thus is relatively new.

Fracture mechanics should attempt to provide quantitative answers to the following questions:

1. What is the strength of the component as a function of crack size?

2. What crack size can be tolerated under service loading, i.e. what is the maximum permissible crack size?

3. How long does it take for a crack to grow from a certain initial size, for example the minimum detectable crack size, to the maximum permissible crack size?

4. What is the service life of a structure when a certain pre-existing flaw size (e.g. a manufacturing defect) is assumed to exist?

5. During the period available for crack detection how often should the structure be inspected for cracks?

Linear elastic fracture mechanics

Griffith's criterion

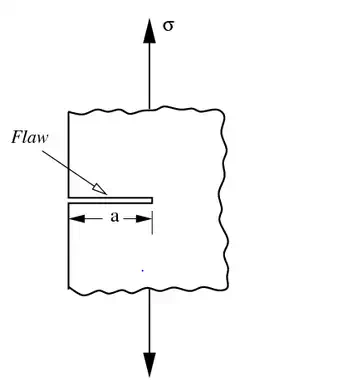
An edge crack (flaw) of length  a in a material

Fracture mechanics was developed during World War I by English aeronautical engineer A. A. Griffith – thus the term Griffith crack – to explain the failure of brittle materials.[3] Griffith's work was motivated by two contradictory facts:

· The stress needed to fracture bulk glass is around 100 MPa (15,000 psi).

· The theoretical stress needed for breaking atomic bonds of glass is approximately 10,000 MPa (1,500,000 psi).

A theory was needed to reconcile these conflicting observations. Also, experiments on glass fibers that Griffith himself conducted suggested that the fracture stress increases as the fiber diameter decreases. Hence the uniaxial tensile strength, which had been used extensively to predict material failure before Griffith, could not be a specimen-independent material property. Griffith suggested that the low fracture strength observed in experiments, as well as the size-dependence of strength, was due to the presence of microscopic flaws in the bulk material.

To verify the flaw hypothesis, Griffith introduced an artificial flaw in his experimental glass specimens. The artificial flaw was in the form of a surface crack which was much larger than other flaws in a specimen. The experiments showed that the product of the square root of the flaw length (a) and the stress at fracture (σf) was nearly constant, which is expressed by the equation:

An explanation of this relation in terms of linear elasticity theory is problematic. Linear elasticity theory predicts that stress (and hence the strain) at the tip of a sharp flaw in a linear elastic material is infinite. To avoid that problem, Griffith developed a thermodynamic approach to explain the relation that he observed. The growth of a crack, the extension of the surfaces on either side of the crack, requires an increase in the surface energy. Griffith found an expression for the constant C in terms of the surface energy of the crack by solving the elasticity problem of a finite crack in an elastic plate. Briefly, the approach was:

· Compute the potential energy stored in a perfect specimen under a uniaxial tensile load.

· Fix the boundary so that the applied load does no work and then introduce a crack into the specimen. The crack relaxes the stress and hence reduces the elastic energy near the crack faces. On the other hand, the crack increases the total surface energy of the specimen.

· Compute the change in the free energy (surface energy − elastic energy) as a function of the crack length. Failure occurs when the free energy attains a peak value at a critical crack length, beyond which the free energy decreases as the crack length increases, i.e. by causing fracture. Using this procedure, Griffith found that

.

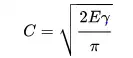
Griffith's criterion has been used by Johnson, Kendall and Roberts also in application to adhesive contacts. Recently, it was shown that direct application of the Griffith criterion to a single numerical "cell" leads to a very robust formulation of the Boundary Element Method.

Irwin's modification

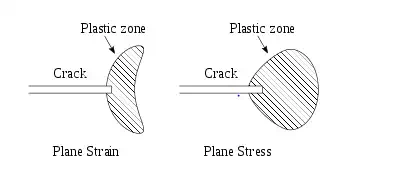
The plastic zone around a crack tip in a ductile material

Griffith's work was largely ignored by the engineering community until the early 1950s. The reasons for this appear to be (a) in the actual structural materials the level of energy needed to cause fracture is orders of magnitude higher than the corresponding surface energy, and (b) in structural materials there are always some inelastic deformations around the crack front that would make the assumption of linear elastic medium with infinite stresses at the crack tip highly unrealistic. 

Irwin's strategy was to partition the energy into two parts:

· the stored elastic strain energy which is released as a crack grows. This is the thermodynamic driving force for fracture.

· the dissipated energy which includes plastic dissipation and the surface energy (and any other dissipative forces that may be at work). The dissipated energy provides the thermodynamic resistance to fracture. Then the total energy is

For brittle materials such as glass, the surface energy term dominates and  For ductile materials such as steel, the plastic dissipation term dominates and {\displaystyle For polymers close to the glass transition temperature, we have intermediate values of G between 2 and 1000 J/m2.