Froude number
In continuum mechanics, the Froude number (Fr) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). Named after William Froude the Froude number is based on the speed–length ratio which he defined as:
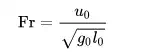
where u0 is a characteristic flow velocity, g0 is in general a characteristic external field, and l0 is a characteristic length. The Froude number has some analogy with the Mach number. In theoretical fluid dynamics the Froude number is not frequently considered since usually the equations are considered in the high Froude limit of negligible external field, leading to homogeneous equations that preserve the mathematical aspects. For example, homogeneous Euler equations are conservation equations.
However, in naval architecture the Froude number is a very significant figure used to determine the resistance of a partially submerged object moving through water. Dynamics of vessels that have the same Froude number are easily compared as they produce a similar wake, even if their size or geometry are otherwise different.
Origins
In open channel flows, Bélanger (1828[4]) introduced first the ratio of the flow velocity to the square root of the gravity acceleration times the flow depth. When the ratio was less than unity, the flow behaved like a fluvial motion (i.e., subcritical flow), and like a torrential flow motion when the ratio was greater than unity.

The hulls of swan (above) and raven (below). A sequence of 3, 6, and 12 (shown in the picture) foot scale models were constructed by Froude and used in towing trials to establish resistance and scaling laws. Quantifying resistance of floating objects is generally credited to William Froude, who used a series of scale models to measure the resistance each model offered when towed at a given speed. Froude's observations led him to derive the Wave-Line Theory which first described the resistance of a shape as being a function of the waves caused by varying pressures around the hull as it moves through the water. The naval constructor Ferdinand Reech had put forward the concept in 1852 for testing ships and propellers. Speed–length ratio was originally defined by Froude in his Law of Comparison in 1868 in dimensional terms as:
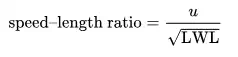
where:
u = flow speed
LWL = length of waterline
The term was converted into non-dimensional terms and was given Froude's name in recognition of the work he did. In France, it is sometimes called Reech–Froude number after Ferdinand Reech.
To show how the Froude number is linked to general continuum mechanics and not only to hydrodynamics we start from the nondimensionalisation of Cauchy momentum equation.
Cauchy momentum equation
In order to make the equations dimensionless, a characteristic length r0, and a characteristic velocity u0, need to be defined. These should be chosen such that the dimensionless variables are all of order one. The following dimensionless variables are thus obtained:

Cauchy-type equations in the high Froude limit Fr → ∞ (corresponding to negligible external field) are named free equations. On the other hand, in the low Euler limit Eu → 0(corresponding to negligible stress) general Cauchy momentum equation becomes an inhomogeneous Burgers equation (here we make explicit the material derivative):

This is an inhomogeneous pure advection equation, as much as the Stokes equation is a pure diffusion equation.
Euler momentum equation
Euler momentum equation is a Cauchy momentum equation with the Pascal law being the stress constitutive relation:
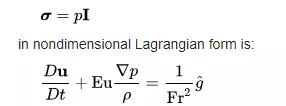
Free Euler equations are conservative. The limit of high Froude numbers (low external field) is thus notable and can be studied with perturbation theory.
Incompressible Navier–Stokes momentum equation
Incompressible Navier–Stokes momentum equation is a Cauchy momentum equation with the Pascal law and Stokes's law being the stress constitutive relations:
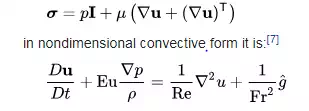
where Re is the Reynolds number. Free Navier–Stokes equations are dissipative (non conservative).