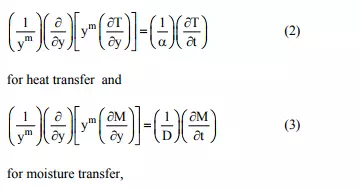HEAT AND MASS TRANSFER DURING MICROWAVE DRYING OF FOOD PRODUCTS

INTRODUCTION

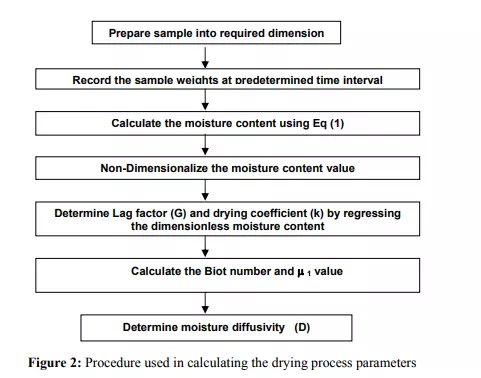
Drying is a complex process involving simultaneous coupled transient heat, mass and momentum transport. It is a process whereby the moisture is vaporized and swept away from the surface, sometimes in vacuum but normally by means of a carrier fluid passing through or over the moist object. This process has found industrial application various forms ranging from wood drying in the lumber industry to food drying in the food industry. In drying process, the heat may be added to the object from an external source by convection, conduction or radiation, or the heat can be generated internally within the solid body by means of electric resistance (Sahin et al., 2002). The effectiveness of a drying process depends on different factors: method of heat transfer, continuity or discontinuity of the process, direction of the heating fluids with respect to the product (pressure atmospheric, low, deep vacuum).Drying process can be performed by using different kinds of equipment such as: air cabinet, belt drier, tunnel drier, fluidized bed, spray drier, drum dryer, foam drier, freeze-drier, microwave oven (Severini et al., 2005). Microwaves with their ability to rapidly heat materials are commonly used as a source of heat. In recent years, microwave drying has gained popularity as an alternative drying method in the food industry. The food industry is the largest consumer of microwave energy, where it can be employed for cooking, thawing, tempering, drying, freeze-drying, and sterilization, baking, heating and re-heating (Cui et al., 2004). Microwave drying is rapid, more uniform and energy efficient compared to conventional hot air drying. Other advantages of microwave drying include space savings and energy efficiency, since most of the electromagnetic energy is converted into heat. Another advantage of microwave application for drying is the internal heat generation. In microwave processing the energy is transferred directly to the sample producing a volumetric heating (Oliveira et al., 2002). There have bean several experimental and theoretical studies on the analysis of heat and moisture transfer during drying of food products and on the determination of mass transfer characteristics such as moisture diffusion and mass transfer coefficient, undertaken by several researchers and engineers (Cohen et al., 1995; Ruiz Dıaz et al. 2003; Karathanos et al. 1999; Zogzas et al. 1996; and Krokida et al. 2001). The objective of any drying process is to produce a dried product of desired quality at minimum cost and maximum throughput possible (Dincer, 1998; Kechaou et al., 2000; and Khraisheh, 1995). Microwave drying could be rapid, more uniform and energy efficient compared to conventional hot air drying (Haghi, 2001; Haghi, 2001; and Haghi, 2005). Krokida et al. (2001) investigated the effects of different drying methods on the colour of the obtained products. They found that colour characteristics are significantly affected by the drying methods. Zogzas et al. (1996) presented a review of reported experimental moisture diffusivity data in food materials.

Dincer and Dost (1995; 1996) developed new analytical models in a simple and accurate manner to determine the mass transfer characteristics for the geometrically shaped products. They also introduced new drying parameters in terms of drying coefficient and lag factors. Sahin et al. (2002) presented a simple model of moisture transfer for multidimensional products. By considering the analogy between the heat diffusion and moisture transfer, drying time for infinite slab products was formulated. The analysis then extended to multidimensional products through the geometric shape factors introduced. Sharma et al. (2004) determined the effective moisture diffusivity of garlic cloves during a microwave-convective drying process. They also investigate its dependence on factors such as microwave power, air temperature and air velocity that essentially influences drying rates. McMinn et al. (2003) determined the mass transfer characteristics for potato slab and cylinders subjected to convection, microwave and microwaveconvective drying by adopting the analytical model proposed by Dincer and Dost. They have shown that the model is an effective means by which to calculate the mass transfer characteristics, also the result show that the power of the microwave has the main effect in drying. In the present work, experimental data from a microwave drying system are used to determine the mass transfer characteristics for slab potato samples by adopting the analytical model developed by Dincer and Dost. Also a prediction model was presented by using factorial technique method for investigate the effect of microwave power and sample’s dimensions on the drying characteristics. The model was applied successfully in the case of potato. The result shown the microwave power has the main effect and increase the dimensions of sample increase the drying time.

EXPERIMENTAL

Experimental Setup

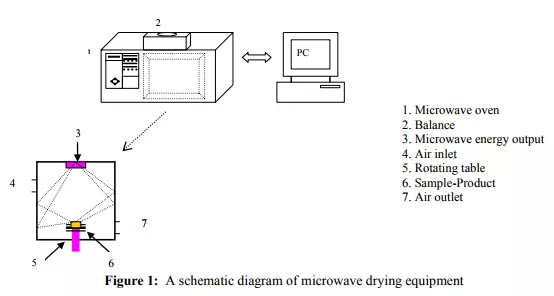
The drying system used in this work was a microwave oven (Butan, model no. MF 45) of variable power output settings and rated capacity of 900 W at 2.45 GHz, outside dimensions (WxDxH), 601x465x338 mm and cavity dimensions (WxDxH), 419x428x245 mm. a schematic diagram microwave dryer is shown in Fig 1.

Material

Trials were performed on potato tubers (It should be noted that composition of potato tubers depends upon generic and climatic factors (Khraisheh et al.; 1995). This may lead to some variations in the moisture content of potatoes within and between varieties. All potato tubers were washed in lukewarm water, hand-peeled and cut into required dimensions.

Drying Procedure

In all experiments, the microwave oven was brought to the operating temperature by heating 1000 ml of distilled water in a glass beaker for 5 min before the first run of the day .The potato samples was placed on Petri dishes in the center of the microwave oven cavity. Throughout the experimental run the sample weights were continuously recorded at predetermined time intervals until no discernible difference between subsequent readings was observed. The moisture content value was determined as:

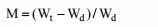
where M is moisture content, Wt is the weight of sample (g) at any time and Wd is the weight of the dried sample.

ANALYSIS OF HEAT AND MOISTURE TRANSFER

A complete drying profile consists of two stages: a constant-rate period and a falling-rate period (19). It is frequently agreed that the mechanism of moisture movement within a hygroscopic solid during the falling-rate period could be represented by diffusion phenomenon according to Fick’s second low. The governing Fickian equation is exactly in the form of the Fourier equation of heat transfer, in which temperature and thermal diffusivity are replaced with concentration and moisture diffusivity, respectively. Therefore, similar to the case of unsteady heat transfer, one can consider three different situations for the unsteady moisture diffusion, namely, the cases where the Biot number has the following values:Bi 0.1 ≤ , 0.1 Bi 100 < < , and Bi 100 > . The first case, corresponding to situations where Bi ≤ 0.1, imply negligible internal resistance to the moisture diffusivity within the solid object. On the other hand, cases where Bi 100 > , including negligible surface resistance to the moisture transfer at the solid object, are the most common situation, while cases where 0.1 Bi 100 < < , including the finite internal and surface resistances to the moisture transfer, exist in practical applications. The time-dependent heat and moisture transfer equations in Cartesian, cylindrical, and spherical coordinates for an infinite slab, infinite cylinder, and a sphere, respectively, can be written in the following compact form (Sahin et al., 2002):