Centre of Gravity

INTRODUCTION

It has been established, since long, that every particle of a body is attracted by the earth towards its centre. The force of attraction, which is proportional to the mass of the particle, acts vertically downwards and is known as weight of the body. As the *distance between the different particles of a body and the centre of the earth is the same, therefore these forces may be taken to act along parallel lines. We have already discussed in Art. 4.6 that a point may be found out in a body, through which the resultant of all such parallel forces act. This point, through which the whole weight of the body acts, irrespect of its position, is known as centre of gravity (briefly written as C.G.). It may be noted that every body has one and only one centre of

gravity.

CENTROID

The plane figures (like triangle, quadrilateral, circle etc.) have only areas, but no mass. The centre of area of such figures is known as centroid. The method of finding out the centroid of a figure is the same as that of finding out the centre of gravity of a body. In many books, the authors also write centre of gravity for centroid and vice versa.

METHODS FOR CENTRE OF GRAVITY

The centre of gravity (or centroid) may be found out by any one of the following two methods:

1. By geometrical considerations

2. By moments

3. By graphical method

As a matter of fact, the graphical method is a tedious and cumbersome method for finding out the centre of gravity of simple figures. That is why, it has academic value only. But in this book, we shall discuss the procedure for finding out the centre of gravity of simple figures by geometrical considerations and by moments one by ones.

CENTRE OF GRAVITY BY GEOMETRICAL CONSIDERATIONS

The centre of gravity of simple figures may be found out from the geometry of the figure as given below.

1. The centre of gravity of uniform rod is at its middle point.

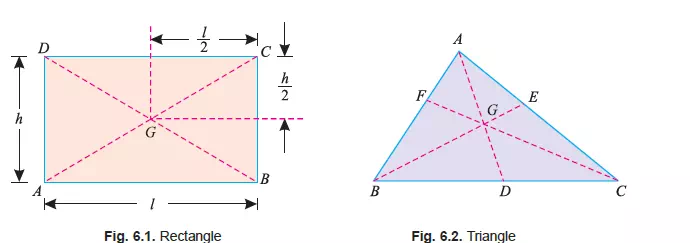
2. The centre of gravity of a rectangle (or a parallelogram) is at the point, where its diagonals meet each other. It is also a middle point of the length as well as the breadth of the rectangle

as shown in Fig. 6.1.

3. The centre of gravity of a triangle is at the point, where the three medians (a median is a line connecting the vertex and middle point of the opposite side) of the triangle meet as

shown in Fig. 6.2.

4. The centre of gravity of a trapezium with parallel sides a and b is at a distance of

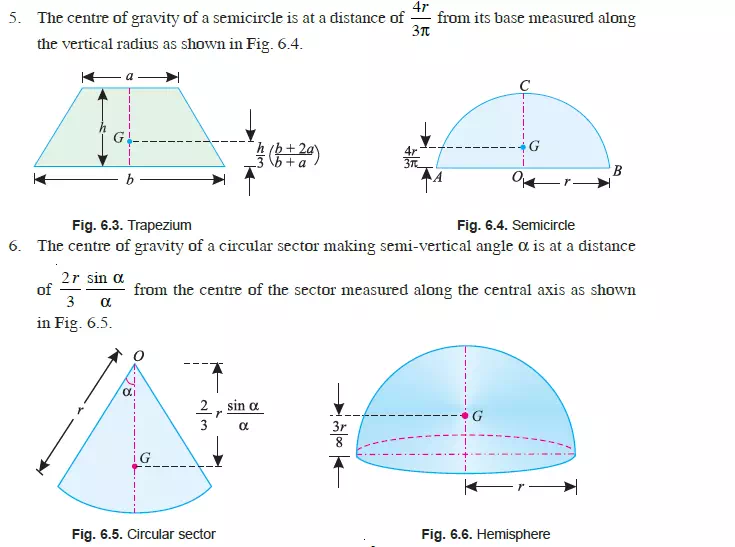
CENTRE OF GRAVITY BY MOMENTS

The centre of gravity of a body may also be found out by moments as discussed below:

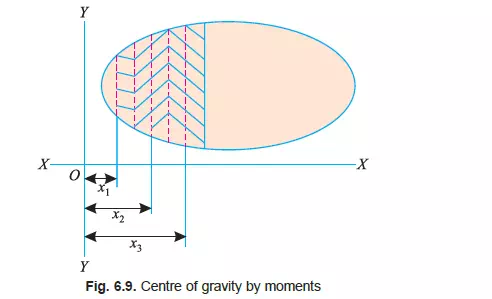
CENTRE OF GRAVITY OF PLANE FIGURES

The plane geometrical figures (such as T-section, I-section, L-section etc.) have only areas but no mass. The centre of gravity of such figures is found out in the same way as that of solid bodies. The centre of area of such figures is known as centroid, and coincides with the centre of gravity of the figure. It is a common practice to use centre of gravity for centroid and vice versa.