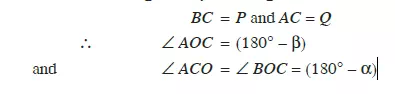Equilibrium of Forces

INTRODUCTION

In the previous chapter, we have discussed the various methods of finding out resultant force, when a particle is acted upon by a number of forces. This resultant force will produce the same effect as produced by all the given forces. A little consideration will show, that if the resultant of a number of forces, acting on a particle is zero, the particle will be in equilibrium. Such a set

of forces, whose resultant is zero, are called equilibrium forces. The force, which brings the set of forces in equilibrium is called an equilibrant. As a matter of fact, the equilibrant is equal to

the resultant force in magnitude, but opposite in direction.

PRINCIPLES OF EQUILIBRIUM

Though there are many principles of equilibrium, yet the following three are important from the subject point of view :

1. Two force principle. As per this principle, if a body in equilibrium is acted upon by two forces, then they must be equal, opposite and collinear.

2. Three force principle. As per this principle, if a body in equilibrium is acted upon by three forces, then the resultant of any two forces must be equal, opposite and collinear with the third force.

3. Four force principle. As per this principle, if a body in equilibrium is acted upon by four forces, then the resultant of any two forces must be equal, opposite and collinear with the resultant of the other two forces.

METHODS FOR THE EQUILIBRIUM OF COPLANAR FORCES

Though there are many methods of studying the equilibrium of forces, yet the following are important from the subject point of view :

1. Analytical method.

2. Graphical method.

ANALYTICAL METHOD FOR THE EQUILIBRIUM OF COPLANAR FORCES

The equilibrium of coplanar forces may be studied, analytically, by Lami’s theorem as discussed below :

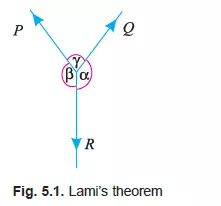
LAMI’S THEOREM

It states, “If three coplanar forces acting at a point be in equilibrium, then each force is proportional to the sine of the angle between the other two.” Mathematically,

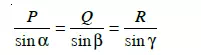
where, P, Q, and R are three forces and á, â, ã are the angles as shown in Fig. 5.1.

Proof

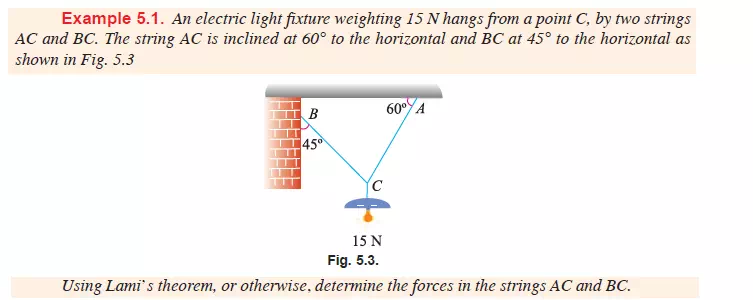
Consider three coplanar forces P, Q, and R acting at a point O. Let the opposite angles to three forces be á , â and ã as shown in Fig. 5.2. Now let us complete the parallelogram OACB with OA

and OB as adjacent sides as shown in the figure. We know that the resultant of two forces P and Q will be given by the diagonal OC both in magnitude and direction of the parallelogram OACB.

Since these forces are in equilibrium, therefore the resultant of the forces P and Q must be in line with OD and equal  to R, but in opposite direction. From the geometry of the figure, we find