Balancing of Rotating Masses

INTRODUCTION

We have already discussed in the last chapter about the centrifugal force. We know that whenever a body is rotating or attached to a rotating shaft, it is subjected to centrifugal force. This force tends to bend the shaft and produce vibrations in it. These dynamic forces not only increase the loads on bearings and stresses in the various members, but also produce unpleasant and even dangerous vibrations. It is therefore, very essential that all rotating bodies should be completely balanced as far as possible.

METHODS FOR BALANCING OF ROTATING MASSES

We have already discussed that whenever a body of some mass is attached to a rotating shaft, it exerts some centrifugal force, whose effect is to bend the shaft, and to produce unpleasant vibrations in it. In order to prevent the effect of centrifugal force, another body is attached to the opposite side of the shaft, at such a position, so as to balance the effect of centrifugal force of the first body. This is done in such a way that the centrifugal force of both the bodies are made to be equal and opposite. The process of providing the second body, in order to counteract the effect of the centrifugal force of the first body, is called balancing of rotating masses.

TYPES OF BALANCING OF ROTATING MASSES

Though there are many types of balancing of rotating masses yet the following are important from the subject point of view :

1. Balancing of a single rotating mass.

2. Balancing of several rotating masses.

BALANCING OF A SINGLE ROTATING MASS

A disturbing mass, attached to a rotating shaft, may be balanced in a number of ways. But the following two are important from the subject point of view :

1. Balancing by another mass in the same plane.

2. Balancing by two masses in different planes.

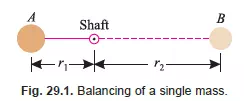
BALANCING OF A SINGLE ROTATING MASS BY ANOTHER MASS IN THE SAME PLANE

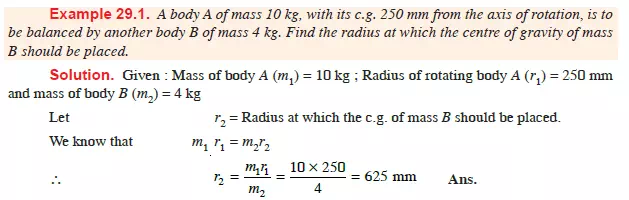
BALANCING OF A SINGLE ROTATING MASS BY TWO MASSES IN DIFFERENT PLANES

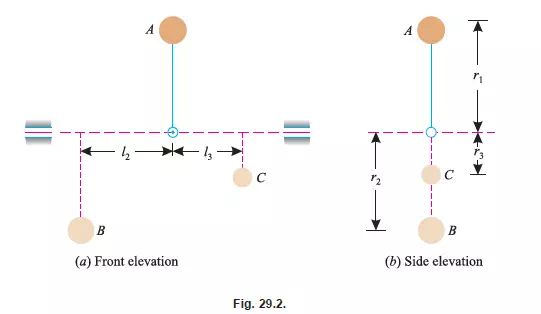
In the previous article, we have discussed the method of balancing of a single rotating body by another mass in the same plane. But sometimes, it is not possible to introduce one balancing mass in the same plane of rotation. In such a case, two balancing masses are provided in two different planes (one on either side of the body to be balanced). In such a case, the following two conditions should be  satisfied in order to balance the body completely :

1. The resultant of all the centrifugal forces (or assumed forces) must be equal to zero.

2. The resultant of moments of all the centrifugal forces (or assumed forces) must be equal to zero. Or in other words, the c.g. of the balancing bodies should lie on the line of action

of the body to be balanced.

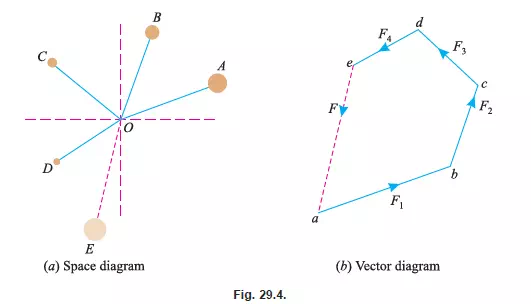
GRAPHICAL METHOD FOR THE BALANCING OF SEVERAL ROTATING MASSES IN ONE PLANE BY ANOTHER MASS IN THE SAME PLANE