Motion Along a Circular Path

INTRODUCTION

We see that whenever a person, drives round a curve or a circular track on a bicycle or a motor cycle or a scootor, he has to lean inward in order to maintain a perfect equilibrium.

As a matter of fact, the angle at which the man leans with the vertical, is more, if he is running at a faster speed than that when he is running at a lower speed. This type of motion is called motion along a circular path.

CENTRIPETAL ACCELERATION

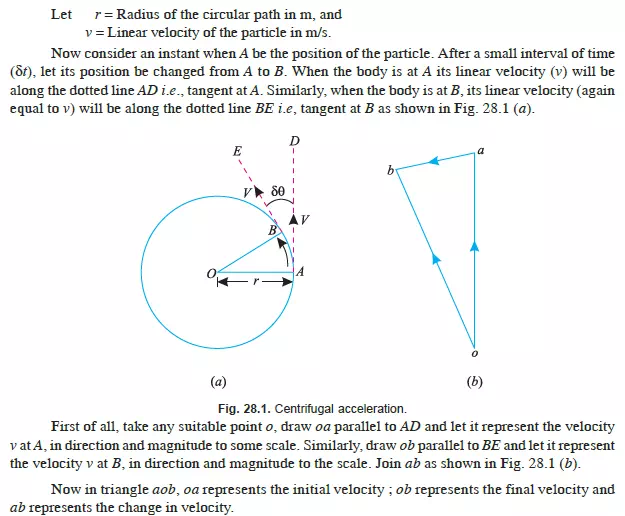
Consider a particle moving along the circumference of a circle with O as centre as shown in Fig. 28.1 (a)

CENTRIPETAL FORCE

A body, moving in a circle or along a circular path, with a constant velocity, suffers a continuous change in its direction at every point of its motion ; though the magnitude of its speed remains the same. Since the velocity involves both magnitude as well as direction, and the velocity of the body is continuously changing due to change in direction ; therefore according to *Newton’s First Law of Motion, an external force must act continuously upon the body, to produce a change in the direction of the moving body. Strictly speaking the body, due to inertia, tends to move along the tangent at every point of its motion, with the constant velocity. Therefore, some force must act at right angles to the direction of motion at every point, which should change the direction of motion of the body, leaving the speed uniform. Thus the force, which acts along the radius of the circle at every point, and is always directed towards the centre of the circle along which the body moves, is known as centripetal force.

CENTRIFUGAL FORCE

According to **Newton’s Third Law of Motion, the force, which acts opposite to the centripetal force, is known as centrifugal force. It may be noted that the centrifugal force always acts away

from the centre of the path, or in other words, the centrifugal force always tends to throw the body away from the centre of circular path.

CENTRIFUGAL FORCE ACTING ON A BODY MOVING ALONG A CIRCULAR PATH

SUPERELEVATION

In our day to day life, we see that whenever a roadway (or railway) is laid on a curve or curved path, then both the edges are not at the same level. In such a case, the outer edge is always higher than the inner one. This is done to keep the vehicle in equilibrium while going on the curved path. We know that the body, moving along a curved path, is subjected to the following forces :

1. Its own weight, and

2. Centrifugal force.

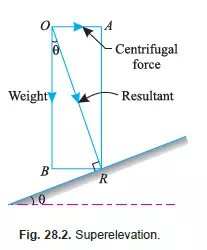
The resultant of these forces is inclined with the vertical as shown in Fig 28.2. It may be noted, that if curved path be made level, then the resultant force will be inclined at some angle, with

the vertical, and thus the reactions on both the supports, of a vehicle, will not be equal, which will effect the equilibrium of the vehicle. To counterbalance this effect and maintain equilibrium

of the vehicle, the surface of the path is made perpendicular to the  resultant by keeping the inner edge level and raising the *outer edge of the roadway or (outer rail of the railway). The amount by which the outer edge of rail is raised is known as cant or superelevation. Now we shall discuss the effect of superelevation in case of roadways and railways in the following pages.

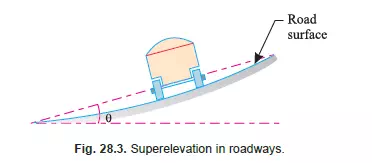
EFFECT OF SUPERELEVATION IN ROADWAYS

In case of roadways, the outer edge is raised with respect to the inner edge of the road surface. The amount, by which the outer edge is raised is known as cant or superelevation. The process of providing superelevation is known as banking of the road. The general practice, to define the superelevation, is to mention the angle of inclination of the road surface as shown in Fig. 28.3. Now consider a vehicle moving on a roadway and along a curved path with a uniform velocity as shown in Fig. 28.3.

* In some countries the outer edge is raised from the centre line by half of the superelevation, and the inner edge is also lowered from the centre line by half of the superelevation.