Motion of Connected Bodies
INTRODUCTION
In the previous chapter, we discussed the motion of a body, when it is subjected to some external force. But in this chapter, we shall discuss the motion of a body, when it is connected by a string to another body, which is subjected to some external force. A little consideration will show, that in this case the velocity and acceleration of both the bodies will be the same. Now in this chapter, we shall discuss the following cases :
1. Two bodies connected by a string and passing over a smooth pulley.
2. Two bodies connected by a string one of which is hanging free and the other lying on a horizontal plane.
3. Two bodies connected by a string one of which is hanging free and the other lying on an inclined plane.
4. Two bodies connected by a string and lying on two inclined planes.
MOTION OF TWO BODIES CONNECTED BY A STRING AND PASSING OVER A SMOOTH PULLEY
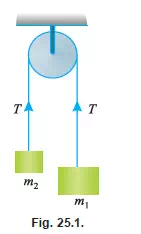
Consider two bodies of masses m1 and m2 kg respectively connected by an inextensible light string (i.e., its weight is neglected) and passing over a small smooth fixed pulley as shown in Fig. 25.1. It may be noted that if the string is light (i.e. its weight is neglected) the tension will be the same throughout its length. But if the string is heavy (i.e., its weight is considered) the tension will vary, depending upon the weight per unit length. Moreover, if the string is extensible the tension will also vary with the extension. It may also be noted that if the string passes over a smooth pulley, the tension will be the same on both sides. But if the string does not pass over a smooth pulley, the tension, in the two strings will also vary. For simplicity, we shall consider light inextensible string passing over a smooth pulley, so that the tension in both the strings may be the same. Let m1 be greater than m2. A little consideration will show, that the greater
mass m1 will move downwards, whereas the smaller one will move upwards. Since the string is inextensible, the upward acceleration of the mass m2 will be equal to the downward
acceleration of the mass m1.
Let a = Acceleration of the bodies and
T = Tension in both the strings.


MOTION OF TWO BODIES CONNECTED BY A STRING, ONE OF WHICH IS HANGING FREE AND THE OTHER LYING ON A SMOOTH HORIZONTAL PLANE
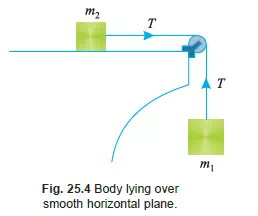
Consider two bodies of masses m1 and m2 kg respectively connected by a light inextensible string as shown in Fig. 25.4. Let the body of mass m1 hang free and the body of mass m2 be placed on a smooth (i.e., friction between the body of mass m2 and the horizontal plane is neglected) horizontal plane. It may be noted that the body of mass m1 will move downwards and the body of mass m2 along the surface of the plane.
We know that velocity and acceleration of the body of mass m1 will be the same as that of the body of mass m2. Since the string is inextensible, therefore, tension in both the strings will also be equal, Let a = Acceleration of the system and T = Tension in the strings

MOTION OF TWO BODIES CONNECTED BY A STRING, ONE OF WHICH IS HANGING FREE AND THE OTHER LYING ON A ROUGH HORIZONTAL PLANE
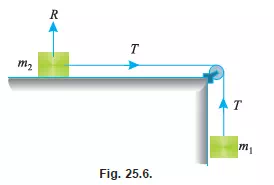
Consider two bodies of masses m1 and m2 kg respectively, connected by a light inextensible string as shown in Fig. 25.6. Let the body of mass m1 hang free, and the body of mass m2 be placed on a rough horizontal plane. Let the body of mass m1 move downwards and the body of mass m2 move along the surface of the plane. We know that velocity and acceleration of the body of mass m1 will be the same as that of mass m2. Since the string is inextensible, therefore tensions in both the strings will also be equal.
Let a = Acceleration of the system,
T = Tension in the string and
́ = Coefficient of friction.
We know that the normal reaction on the horizontal surface due to body of mass m2 kg (as shown in Fig. 25.6)


MOTION OF TWO BODIES CONNECTED BY A STRING, ONE OF WHICH IS HANGING FREE AND OTHER LYING ON A SMOOTH INCLINED PLANE
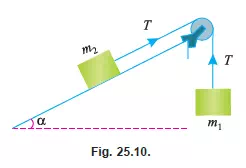
Consider two bodies of masses m1 and m2 kg respectively connected by a light inextensible string as shown in Fig. 25.10. Let the body of mass m1 hang free and the body of mass m2 be placed on an inclined smooth plane (i.e., the friction between the mass m2 and the plane is neglected). It may be noted that the body of mass m1 will move downwards and the body of mass m2 will move upwards along the inclined surface. A little consideration will show that the velocity and acceleration of the body of mass m1 will be the same as that of the body of mass m2. Since the string is inextensible, therefore tension in both the strings will also be equal.
Let a = Acceleration of the system
T = Tension in the strings and
á = Inclination of the plane.

