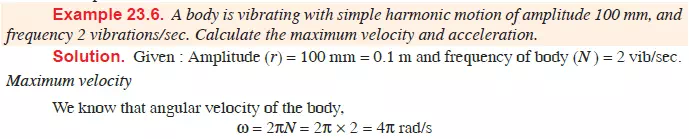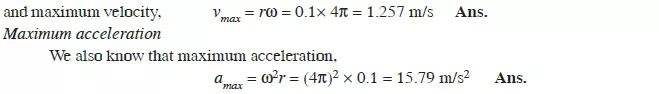Simple Harmonic Motion

INTRODUCTION

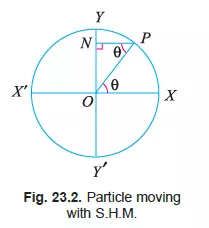
In the previous chapters, we have discussed the motion of particles or bodies in a straight line or in rotation. But in this chapter, we shall discuss the motion of a particle or point along a circular path and its effect on one of its diameters. Consider a particle starting from x and moving round the circumference of circle in an anti-clockwise direction, with a constant angular velocity, as shown in Fig. 23.1. Let P be the position of the particle at any instant and N be the projection of P on the diameter Y-Y' of the circle. It will be interesting to know that when the point P moves round the circumference of the circle from x to y, N moves from O to y ; when P moves from y to x', N moves from y to O. Similarly, when P moves from x' to y', N moves from O to y', and finally when P moves from y' to x, N moves from y' to O. Hence, as P completes one revolution, the point N completes one vibration about the point O. This to and fro motion of N is known as Simple harmonic motion, briefly written as S.H.M.

IMPORTANT TERMS

The following terms, which will be frequently used in this chapter, should be clearly understood at this stage :

1. Amplitude. It is the maximum displacement of a body, from its mean position. In Fig. 23.1, Oy and Oy' is the amplitude of the particle N. The amplitude is always equal to the radius of the

circle.

2. Oscillation. It is one complete vibration of a body. In Fig. 23.1, when the body moves from y to y' and then back to y (or in other words from O to y, y to y' and then y' to O), it is said to have completed one oscillation.

3. Beat. It is half of the oscillation. In Fig. 23.1, when the body moves from y to y' or y' to y (or in other words O to y' and then y' to O), it is said to have completed one beat.

4. Periodic time. It is the time taken by a particle for one complete oscillation. Mathematically, periodic time,

GENERAL CONDITIONS OF SIMPLE HARMONIC MOTION

In general, a body is said to move or vibrate, with simple harmonic motion, if it satisfies the following two conditions :

1. Its acceleration is always directed towards the centre, known as the point of reference or mean position.

2. Its acceleration is proportional to the distance from that point.

VELOCITY AND ACCELERATION OF A PARTICLE MOVING WITH SIMPLE HARMONIC MOTION

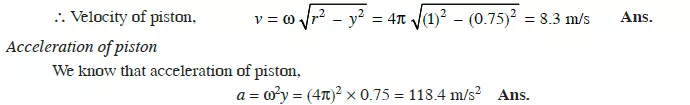
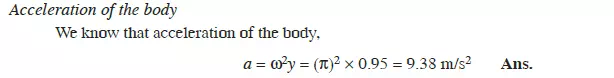
MAXIMUM VELOCITY AND ACCELERATION OF A PARTICLE MOVING WITH SIMPLE HARMONIC MOTION