Projectiles

INTRODUCTION

In the previous chapters, we have been discussing the motion of bodies, either in horizontal or vertical directions. But we see that whenever a particle is projected upwards at a certain angle (but not vertical), we find that the particle traces some path in the air and falls on the ground at a point, other than the point of projection. If we study the motion of the particle, we find that the velocity, with which the particle was projected, has two components namely vertical and horizontal. The function of the vertical component is to project the body vertically upwards, and that of the horizontal is to move the body horizontally in its direction. The combined effect of both the components is to move the particle along a parabolic path. A particle, moving under the combined effect of vertical and horizontal forces, is called a  projectile. It may be noted that the vertical component of the motion is always subjected to gravitational acceleration, whereas the horizontal component remains constant.

IMPORTANT TERMS

The following terms, which will be frequently used in this chapter, should be clearly understood at this stage :

1. Trajectory. The path, traced by a projectile in the space, is known as trajectory.

2. Velocity of projection. The velocity, with which a projectile is projected, is known as the velocity of projection.

3. Angle of projection. The angle, with the horizontal, at which a projectile is projected, is known as the angle of projection.

4. Time of flight. The total time taken by a projectile, to reach maximum height and to return back to the ground, is known as the time of flight.

5. Range. The distance, between the point of projection and the point where the projectile strikes the ground, is known as the range. It may be noted that the range of a projectile

may be horizontal or inclined.

MOTION OF A BODY THROWN HORIZONTALLY INTO THE AIR

Consider a body at A thrown horizontally into the *air with a horizontal velocity (v) as shown in Fig. 20.1. A little consideration will show, that this body is subjected to the following two

velocities :

1. Horizontal velocity (v), and 

2. Vertical velocity due to gravitational acceleration.

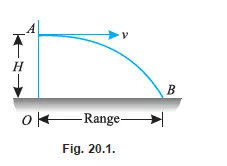
It is thus obvious, that the body will have some resultant  velocity, with which it will travel into the air. We have already discussed in Art 20.1. that the vertical component of this velocity is

always subjected to gravitational acceleration, whereas the horizontal component remains constant. Thus the time taken by the body to reach the ground, is calculated from the vertical component of the velocity, whereas the horizontal range is calculated from the horizontal component of the velocity. The velocity, with which the body strikes the ground at B, is the resultant of horizontal and vertical velocities.

Example 20.1. An aircraft, moving horizontally at 108 km/hr at an altitude of 1000 m towards a target on the ground, releases a bomb which hits it. Estimate the horizontal distance of the

aircraft from the target, when it released the bomb. Calculate also the direction and velocity with which the bomb hits the target. Neglect air friction.

Solution. Given : Horizontal velocity of aircraft, (V) = 108 km/hr = 30 m/s Horizontal distance of the aircraft from the target when it released the bomb First of all, consider the vertical motion of the bomb due to gravitational acceleration only. In this case, initial velocity (u) = 0 and distance covered (s) = 1000 m. Let t = Time required by bomb to reach the ground.

MOTION OF A PROJECTILE

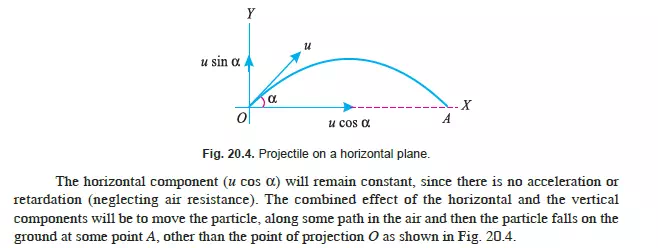
EQUATION OF THE PATH OF A PROJECTILE