Relative Velocity

INTRODUCTION

It has been established since long that every motion is relative, as an absolute motion is impossible to conceive. Strictly speaking, our motion is always relative with reference to the Earth , which is supposed to be fixed or at rest. But we know that our Earth is also not at rest. It has some relative velocity with respect to the celestial bodies such as sun, moon etc. These celestial bodies, in turn, have some relative velocity with respect to the stars of the universe. It will be interesting to know that when we say that a train is moving at 50 kilometres per hour, we

simply mean that the speed of the train, which appears to an observer on the earth, is 50 kilometres per hour. Thus the relative velocity of A with respect to B, is the velocity with which A appears to move to an observer sitting on B, neglecting the motion of B relative to the Earth.

METHODS FOR RELATIVE VELOCITY

The relative velocity of two bodies may be found out either graphically or analytically. But it has been experienced that analytical method is somewhat confusing. Thus in this book, we shall

follow the graphical method. The best practice is the combination of both the methods. The values should first be obtained by graphical method and then their accuracy should be checked analytically.

RELATIVE VELOCITY OF RAIN AND MAN

We see in our daily walk of life, that whenever we go out in rain, we have to adjust the inclination of our umbrella (with the vertical) to protect ourselves from the rain. If the rain is falling in the opposite direction of our movement, then the inclination of umbrella is less when we are standing, than that when we are moving. This happens because the relative velocity of rain (with respect to our movement) now is inclined at a greater angle.

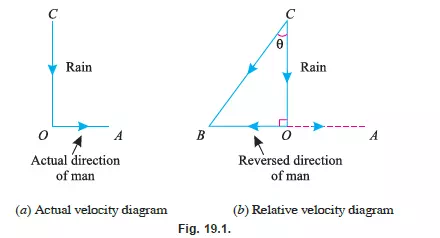
Now consider CO and OA as actual directions of the rain and man respectively as shown in Fig. 19.1 (a). The relative velocity diagram for rain and man may be drawn as shown in Fig. 19.1 (b)

and as discussed below :

1. First of all, draw a horizontal line OA to some suitable scale which represents the actual direction of motion of the man.

2. Now draw CO equal to the velocity of the rain (assumed to be vertical in this case) to the

scale.

3. Let us *superimpose a velocity equal and opposite to that of the man on both the man as

well as rain. It will reduce the velocity of the man to zero. And the rain will have some

resultant velocity (due to its own velocity and superimposed velocity) as shown in Fig.

19.1 (b).

4. Now relative velocity of the rain and man, in magnitude and direction, will be given by the

resultant velocity CB, which may be found out either graphically or by Triangle Law or

Forces.

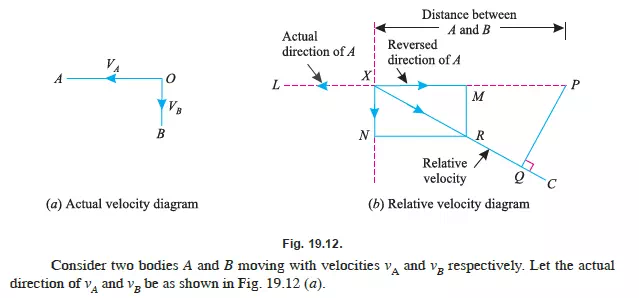
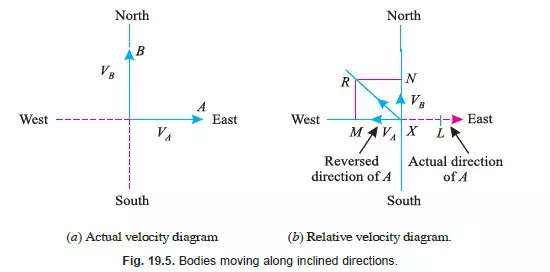
RELATIVE VELOCITY OF TWO BODIES MOVING ALONG INCLINED

DIRECTIONS

Sometimes, two bodies are moving along two inclined directions. In such a case, the relative

velocity of one, with respect to the other, may be found out by superimposing the actual velocity of

any one of these two bodies, in the opposite direction, on both the bodies. It will be interesting to

know that after superimposing the velocity, one of the bodies will be brought to rest. And the resultant

of the two velocities, on the second, will give the required relative velocity.

LEAST DISTANCE BETWEEN THE TWO BODIES MOVING ALONG

INCLINED DIRECTIONS