Support Reactions

INTRODUCTION

In our day-to-day work, we see that whenever we apply a force on a body, it exerts a *reaction, e.g., when a ceiling fan is hung from a girder, it is subjected to the following two forces:

1. Weight of the fan, acting downwards, and

2. Reaction on the girder, acting upwards.

A little consideration will show, that as the fan is in equilibrium therefore, the above two forces must be equal and opposite. Similarly, if we consider the equilibrium of a girder supported on the walls, we see that the total weight of the fan and girder is acting through the supports of the girder on the walls. It is thus obvious, that walls must exert equal and upward reactions at the supports to maintain the equilibrium. The upward reactions, offered by the walls, are known as support reactions. As a mater of fact, the support reaction depends upon the type of loading and the support.

TYPES OF LOADING

Though there are many types of loading, yet the following are important from the subject point of view :

1. Concentrated or point load,

2. Uniformly distributed load,

3. Uniformly varying load.

CONCENTRATED OR POINT LOAD

A load, acting at a point on a beam is known as a concentrated or a point load as shown in Fig. 12.1.

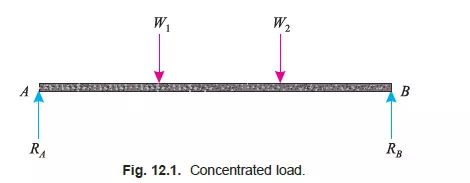
In actual practice, it is not possible to apply a load at a point (i.e., at a mathematical point), as it must have some contact area. But this area being so small, in comparison with the length of the

beam, is negligible.

UNIFORMLY DISTRIBUTED LOAD

A load, which is spread over a beam, in such a manner that each unit length is loaded to the same extent, is known as uniformly distributed load (briefly written as U.D.L.) as shown in Fig. 12.2

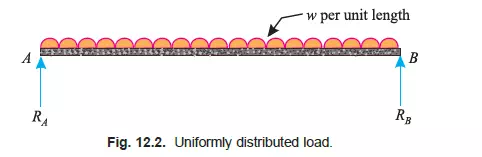
The total uniformly distributed load is assumed to act at the centre of gravity of the load for all sorts of calculations.

UNIFORMLY VARYING LOAD

A load, which is spread over a beam, in such a manner that its extent varies uniformly on each unit length (say from w1 per unit length at one support to w2 per unit length at the other support) is known as uniformly varying load as shown in Fig. 12.3. Sometimes, the load varies from zero at one support to w at the other. Such a load is also called triangular load.

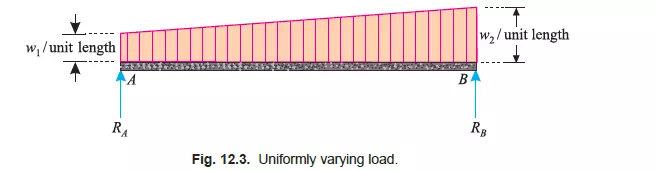
Note : A beam may carry any one of the above-mentioned load system, or a combinations of the two or more.

METHODS FOR THE REACTIONS OF A BEAM

The reactions at the two supports of a beam may be found out by any one of the following two methods:

1. Analytical method 2. Graphical method.

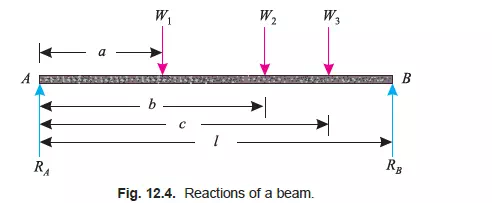
ANALYTICAL METHOD FOR THE REACTIONS OF A BEAM

GRAPHICAL METHOD FOR THE REACTIONS OF A BEAM

It is a systematic, but long method, for finding out the reactions of a beam which is done by the following steps :

1. Construction of space diagram.

2. Construction of vector diagram.

CONSTRUCTION OF SPACE DIAGRAM

It means to construct the diagram of the beam to a suitable scale. It also includes the loads, carried by the beam along with the lines of action of the reactions. Now name the different loads

(or forces) including the two reactions according to Bow’s notations.

CONSTRUCTION OF VECTOR DIAGRAM

After drawing the space diagram of the beam, and naming all the loads or forces according to Bow’s notations as shown in the figure. The next step is to construct the vector diagram. A vector

diagram is drawn in the following steps :

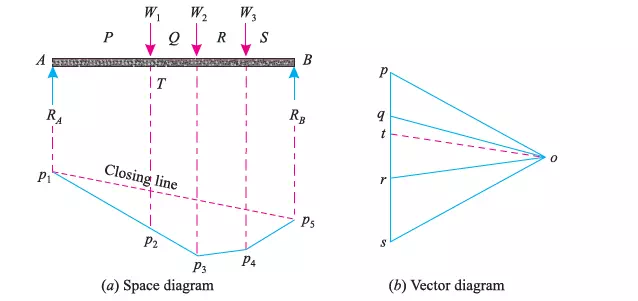
1. Select some suitable point p, near the space diagram and draw pq parallel and equal to the load PQ (i.e.,W1) to some scale.

2. Similarly, through q and r, draw qr and rs parallel and equal to the loads QR and RS (i.e., W2 and W3) to the scale.

3. Select any suitable point o and join op, oq, or and os as shown in Fig. 12.5 (b).

4. Now extend the lines of action of the loads and the two reactions in the space diagram.

5. Select some suitable point p1 on the lines of action of the reaction RA. Through p1 draw p1 p2 parallel to op intersecting the line of action of the load W1 at p2.

6. Similarly, draw p2 p3, p3 p4 and p4 p5 parallel to oq, or and os respectively.

7. Join p1 with p5 and through o draw a line ot parallel to this line.

8. Now the lengths tp and st, in the vector diagram, give the magnitude of the reactions RA and RB respectively to the scale as shown in Figs. 12.5 (a) and (b).

TYPES OF END SUPPORTS OF BEAMS

Though there are many types of supports, for beams and frames, yet the following three types of supports are important from the subject point of view:

1. Simply supported beams,

2. Roller supported beams, and

 3. Hinged beams.