Calculation of braking effort

Weight Transfer:

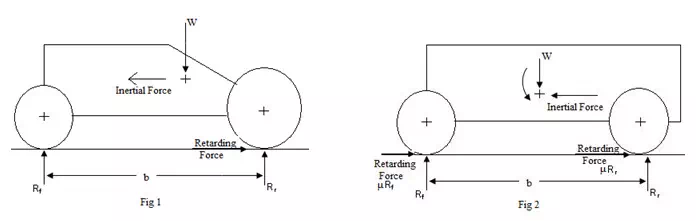
The figure 2 shows a body moving towards the left with an inertial force. Brake is applied, which produces a retarding force at the road surface. This retarding force at the road surface causes an overturning couple on the body due to which weight transfer takes place from the rear to the front wheels.

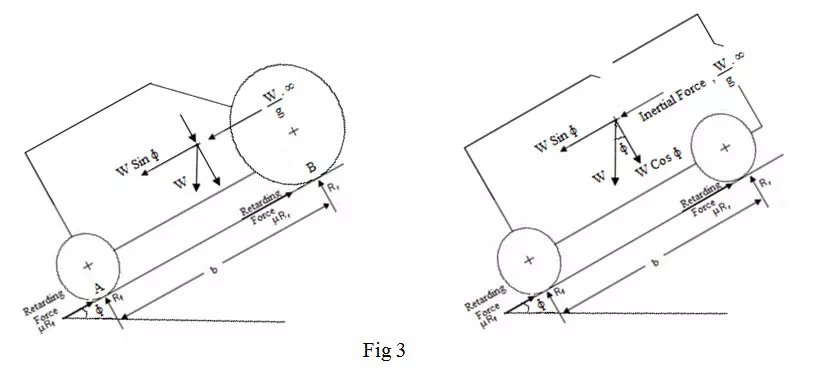
In figure 3, the body is coming down a gradient of angle f when the brakes are applied.

W  = Weight of the vehicle

Rf= Normal reaction on the front wheel

Rr= Normal reaction on the rear wheel

b    = Wheelbase

h    = Height of CG from the surface of the road

∞   = Retarding force due to breaking

μ    = Coefficient of friction between the wheels and the road surface

μRf= Braking force on the front wheels

μRr= Braking force on the rear wheels

When brakes are applied on all the wheels

Rf + Rr = W Cos \[\phi \]                               -1

μRf + μRr = W Sin \[\phi \] + W .∞              -2

                                                  g

In case of equilibrium ∑ M=0 at point B

W . ∞.h + W Sin \[\phi \]. h + W Cos \[\phi \]. x - Rf. b

       g

From equation 1 and 2

            Μ W Cos \[\phi \] = W Sin \[\phi \] + W. ∞

                                                                        g

∞ = μ.Cos \[\phi \] - Sin \[\phi \]                       -4

             g

From equation 3 and 4

            Rf = W(x +μh). Cos \[\phi \]

                              b

            Rr=W(b- x- μh) . Cos \[\phi \]

                                 b

Case of Indian Agricultural Tractors

While most of the automobiles have an all wheel braking but most of the Indian Agricultural Tractors, being rear wheel drive, have braking only in the rear wheels.

The weight transfer in case of tractors with braking in the rear wheels only is analyzed as follows:

Rf + Rr = W Cos \[\phi \]                               -5

μRr = W Sin \[\phi \] + W . ∞                       -6

                                         g

Taking moments above point A

      Rr .b + W.h.Sin \[\phi \] + W . ∞. h – W(b-x)Cos \[\phi \] = 0                    -7

                                             g

From equation 6 and 7

            ∞  =μ(b-x) Cos \[\phi \]      -    Sin \[\phi \]

            g       (b + μh)   

            Rf=W.(b-x). Cos \[\phi \]

                        (b + μh)

            Rr = W(x + μh). Cos \[\phi \]

                        (b + μh)

In case the body (or the tractor) is moving up the slope, the angle of the slope may be taken as negative and the derived expression can be used.