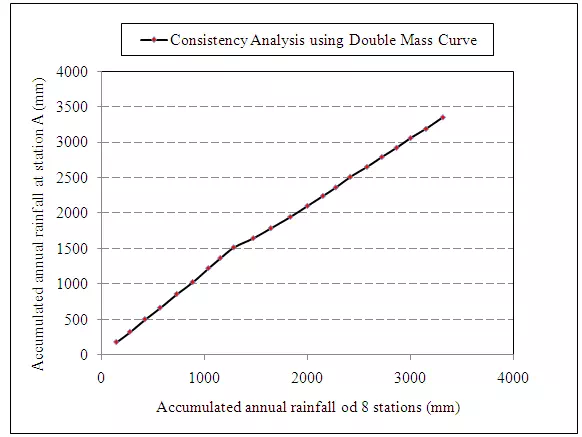
Consistency of Rainfall Record

Consistency of Rainfall Record

Precipitation puts water in the watershed. Precipitation measurements help determine water availability for evaporation and streamﬂow, and the risk of forest ﬁres, landslides, and soil erosion. Precipitation is liquid (rain) or frozen (sleet, hail, graupel, snow) water or a combination of both falling from the sky. Measurement of the accumulation and disappearance of frozen precipitation on the ground is discussed in the following subsection. Precipitation is measured as depth of water that would accumulate on a horizontal surface. Typical recorded values for precipitation are the daily, monthly, and annual totals (depth of water in millimeters), as well as storm total, maximum intensity (millimeters per minute or per hour), and duration (hours). Precipitation is measured at a point using a manual or automatic recording gauge and over an area using meteorological radar (e.g., Doppler) or satellite images. Measurement of rainfall with a gauge is less prone to error than the measurement of solid precipitation because it is less susceptible to the inﬂuence of wind on “catch” by gauges. Some gauges are suitable only for measuring rainfall, and others are used only for solid precipitation. Very few can measure both forms reliably. Precipitation is usually not uniform in spatial distribution, intensity, or duration within a storm. Wind ﬂow interacting with watershed topography also aﬀects the distribution of precipitation. The standard technique for measuring rainfall is a plastic or metal cylinder with a sharp edge and funnel-like cover to minimize evaporation.

Rainfall is measured to the nearest 0.2 mm; an accumulation of less than this is called a “trace.” If these gauges are not measured daily, then a small amount of mineral oil or kerosene is added after each measurement to cover the surface of the water and reduce evaporative loss.

The depth of ﬂuid is measured with a ruler. Precipitation intensity or amount can be measured automatically using weighing gauges or tipping buckets. The latter method is usually restricted to rainfall measurement. The tipping bucket gauge has a pair of buckets that pivot under a funnel such that when one bucket ﬁlls with about 0.25 mm of rain, it tips, discharging its contents and bringing the other bucket under the funnel. Tipping activates a switch that sends a pulse to the recording device. The weighing gauges can have a clock-driven chart to record weight or send an electronic signal to a data logger from a pressure transducer. Weighing gauges used to measure snow, contain antifreeze to melt the snow.

Many studies require long term rainfall data, therefore, a test must be conducted to check homogeneity or self consistency of the rainfall record. This is necessary because over a period of time, it may happen that there be a some obstructions (trees, buildings) may have emerged after the installation of gage or its location might have changed or observational procedure might have changed. The inconsistency of rainfall record can be checked by graphical or statistical methods including double mass curve, the von Neumann ratio test, cumulative deviation, run test. Double mass curve method described below is one of the most common and widely accepted methods for checking the consistency of rainfall record.

Double-mass Curve

This method is based on the assumption that the mean accumulated precipitation for a large group of stations is not significantly affected by a change or changes in individual stations. If we plot the mean accumulated precipitation for several stations against the accumulated precipitation of the record for the station that needs to be adjusted, any change in slope will indicate a “break” in the station record. This is shown by point B in the Fig. for the year 1974. If the slope of the line AB (year 1970-74 in the example) is a and of the line AC (1974-85 in example fig.) is b, the adjustment of the inconsistent data is made by the ration of the slope of two line segments. Two ways of adjustments are possible.

1. The dataadjusted to reflect the conditions that existed prior to the indicated break. This is done by multiplying each recent precipitation value after break point B of station X (being tested) by the ratio a/b.

2. The data are adjusted toreflect recent conditions following the break. This is achieved by multiplying each value of the precipitation before the break by the ratio b/a. Adjustment of this type is generally made.

This is essentially a simple graphical method but statistical concepts and tests can be also utilized. Let us assume that we wish to check whether the data y1, y2 ,..., yN (N= sample size) are consistent data or not. For this purpose we will use another data set N x1, x2... xN, which is known to be reliable. The latter data set could be data measured at another gage or more generally the average of the data records available at several sites located in the same region as the suspected gage y. We will define the cumulative partial sums as

St(Y)=St-1 (Y) + Yt , t = 1,2,…,N

St(X) = St-1 (X) +Xt , t = 1,2,…,N

in which . Thus we have two sequences of partial sums, namely: and . The double mass plot is constructed as shown in the sketch below.

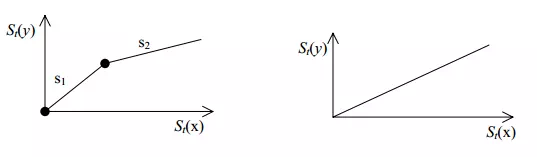
Description: Description: Description: 81
Fig. 8.1(a) Fig. 8.1(b

Figure 1(a) reflects the inconsistency in the data while Fig.1(b) reflects that series yt has a pattern consistent with that of series xt. Referring to Fig.1(a) the point where the slope changes from s1 to s2 marks the time where the inconsistency occurs. Therefore part of the record of y must be adjusted. Which part of the record must be adjusted (before the break point or after) depends on the particular case. For example, if the inconsistency in y has occurred because the gage was moved from the original location to another location (the current location), then it is logical to adjust the record before the break point.

Limitations and Cautions

It is possible that an apparent change in slope is noticed because of a natural variation in the data which is not associated with changes in gage location, gage environment or observation procedure. In the case of doubt, a test of hypothesis should be performed by the Fisher distribution on two data sets (before and after the break) to check whether the data are homogeneous and the break is purely by chance.

If the fewer than 10 stations are grouped together to check the consistency of a station, the record of each station should be tested by double mass analysis for consistency by plotting it against the group of all other stations, and those records that are inconsistent should be eliminated from the group.

This method should seldom be used in mountainous areas. Furthermore, it is also not suitable for adjusting daily or storm precipitation.

Example

Test the consistency of the 22 years of data of the annual precipitation measuredat stationA. Rainfall data for station A as well as the averageannual rainfall measured for a group of eight neighboring stations located in a meteorologicallyhomogeneous region are given below as follows:

Sl. No.	Year	Annual Rainfall of Station A	Average Annual Rainfall (AAR) of 8 Station Group
		(mm)	(mm)
1	1946	177	143
2	1947	144	132
3	1948	178	146
4	1949	162	147
5	1950	194	161
6	1951	168	155
7	1952	196	152
8	1953	144	117
9	1954	150	130
10	1955	130	190
11	1956	141	170
12	1957	160	190
13	1958	155	166
14	1959	140	150
15	1960	120	125
16	1961	148	140
17	1962	142	163
18	1963	140	145
19	1964	130	143
20	1965	137	135
21	1966	130	150
22	1967	163	165

a) In what year is a change in regime indicated?

b) Adjust the record data at a station A and determine the mean annual precipitation.

		Col 3	Col 4	Col 5	Col 6
Sl. No.	Year	Annual Rainfall of Station A	Average Annual Rainfall (AAR) of 8 Station groups	Cumulative Station A rainfall	Cumulative of 8 Station A.A.R.	Correction factor	Adjusted rainfall at station A
		(mm)	(mm)	(mm)	(mm)
1	1946	177	143	177	143	1.18	140.8471
2	1947	144	132	321	275		114.5875
3	1948	178	146	499	421		141.6428
4	1949	162	147	661	568		128.9109
5	1950	194	161	855	729		154.3748
6	1951	168	155	1023	884		133.6854
7	1952	196	152	1219	1036		155.9663
8	1953	144	117	1363	1153		114.5875
9	1954	150	130	1513	1283		119.3619
10	1955	130	190	1643	1473	0.94	196
11	1956	141	170	1784	1643		141
12	1957	160	190	1944	1833		158
13	1958	155	166	2099	1999		145
14	1959	140	150	2239	2149		132
15	1960	120	125	2359	2274		95
16	1961	148	140	2507	2414		148
17	1962	142	163	2649	2577		142
18	1963	140	145	2789	2722		140
19	1964	130	143	2919	2865		130
20	1965	137	135	3056	3000		137
21	1966	130	150	3186	3150		130
22	1967	163	165	3349	3315		163
							139.134

Correction factor: (0.935/1.175)= 0.7957= 0.796 or 0.8

Mean Annual Precipitation

139.134

Description: Description: Description: 82