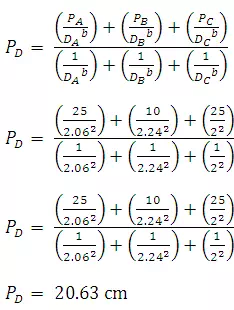Estimation of Missing Rainfall Data
Estimating Missing Data
The point observation from a precipitation gage may have a short break in the record because of instrument failure or absence of the observer. Thus, it is often necessary to estimate the missing record using data from the neighboring station. The following methods are most commonly used for estimating the missing records.
1. Simple Arithmetic Method
2. Normal Ratio Method
3. Modified normal ratio method
4. Inverse distance method
5. Linear programming method
For m stations, 1, 2, 3, …,m, the annual precipitation values are P1, P2, P3, …, Pm, respectively. At station x (not included in the above m stations), the missing annual precipitation (Px) should be found out. The normal annual precipitation N1, N2, N3, …,Ni at each of the above (m+1) stations including the station x is known.
Normal Precipitation - It is the average value of precipitation at a particular date, month or year over a specified 30 year period. Thus, the term normal annual precipitation at station A means the average annual precipitation at A based on a specified 30 year of record.
Simple Arithmetic Average - The missing precipitation Px can be determined using simple arithmetic average, if the normal annual precipitation at various stations are within 10% of the normal precipitation at station, x, as follows:
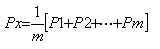 (7.1)
(7.1)
Normal Ratio Method - If the normal precipitations vary considerably then Px is estimated by weighting the precipitation at various stations by the ratios of normal annual precipitation. The normal ration method gives Px as:
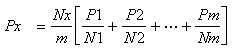 (7.2)
(7.2)
This method is based selecting m (m is usually 3) stations that are near and approximately evenly spaced around the station with the missing record.
Example 1: The normal annual rainfall at stations A, B, C and D in a basin are 80.97, 67.59, 76.28, and 92.01 cm, respectively. In the year 1975, the station D was inoperative and the stations A, B, and C recorded annual rainfall of 91.11, 72.23, and 79.89 cm, respectively. Estimate the rainfall at station D in that year.
Solution: As the normal rainfall values vary by more than 10%, the ration method is adopted.
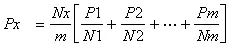
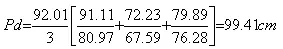
Modified Normal Ratio Method
Normal ratio method is modified to incorporate the effect of distance in the estimation of missing rainfall.
 (7.3)
(7.3)
Where is normal rainfall, is the distance between the index station i and the gauge station with missing data or ungaged station, n is the number of index stations and b is the constant by which the distance is weighted (normally 1.5-2.0) commonly used D0.5
Inverse Distance Method
The inverse distance method has been advocated to be the most accurate method as compare to other two methods discussed above. Amount of rainfall to be estimated at a location is a function of;
1. rainfall measured at the surrounding index stations
2. distance to each index station from the ungauged location
Rainfall rx at station x is given by;
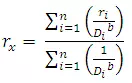 (7.4)
(7.4)
b = 2 is commonly used.
As in inverse distance method the weighting is strictly based on distance, hence this method is not satisfactory for hilly regions.
Example 7.2 Data for the base station and 5 surrounding stations are tabulated below. Find missing data at ‘A’ using (i) modified normal ratio method and (ii) inverse distance method.
|
Station |
Distance (D) from the base station (km) |
Rainfall (cm|) |
Normal Rainfall (cm) |
|
A (base station) |
- |
? |
102 |
|
B |
1.5 |
2.5 |
114 |
|
C |
1.21 |
3.4 |
122 |
|
D |
0.85 |
1.5 |
95 |
|
E |
1.3 |
2.2 |
106 |
|
F |
2.11 |
1.8 |
104 |
Solution: (i) Using modified normal ratio method
Weight calculation for different stations other than the base station is shown in following table, using b = 2
|
Station |
Weight (a) |
|
|
B |
1.22 |
|
|
C |
1.1 |
|
|
D |
0.92 |
|
|
E |
1.14 |
|
|
F |
1.45 |
|
|
Sum |
5.83 |
1.0 |
Hence,
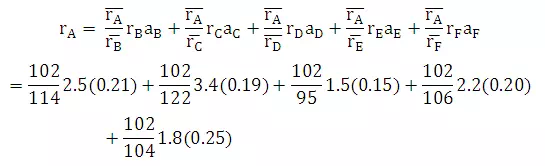
= 2.12 cm
(ii) Using Inverse Distance Method
|
Station |
Weight (a) |
|
|
B |
0.44 |
|
|
C |
0.68 |
|
|
D |
1.38 |
|
|
E |
0.59 |
|
|
F |
0.22 |
|
|
Sum |
3.31 |
1.0 |
Hence,
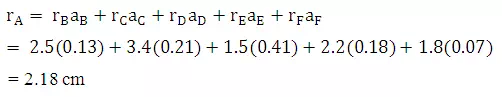
Linear Programming Method
Linear programming (LP) method selects a base station and several surrounding index stations and determines optimal weighting factor by minimizing the deviation between observed and computed rainfall at a base station for a number of rainfall events.
Thus it determines optimal weighting factors for the base station and associated index stations.
This method can be
formulated as,Objective is to
minimize sum of deviation for k events i.e., Minimize 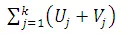
Subjected to
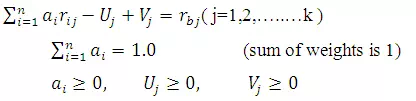
(Non-negativity constraints)
Where, i = index for “index station”
j = index for rainfall events
= observed rainfall at base station ‘b’ for event ‘j’
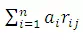 = computed rainfall at base station
for event ‘j’
= computed rainfall at base station
for event ‘j’
For any event, computed rain – observed rain = deviation
Deviation could be either positive or negative value (unrestricted in sign), such variables are replaced by the difference of two non-negative variables (LP requirement) i.e., U.
Solved Example
Assume that rainfall is not known at the station D. The normal precipitations of the three neighbouring gauging stations are as follows:
|
Station |
Station co-ordinate |
Normal Annual Precipitation (cm) |
Precipitation (cm) |
|
|
A |
(1,2.5) |
28 |
25 |
|
|
B |
(4,1) |
15 |
10 |
|
|
C |
(3,5) |
30 |
25 |
|
|
D |
(3,3) |
25 |
? |
|
Compute the rainfall at this point using
a. Simple Arithmetic Method
b. Normal Ratio Method
c. Modified Normal Ratio Method
d. Inverse Distance Method
Answer
a. Simple Arithmetic Method
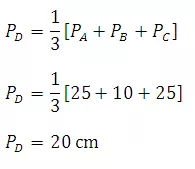
b. Normal Ratio Method
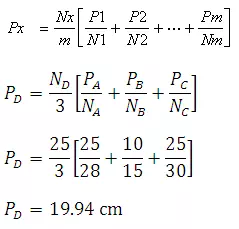
c. Modified Normal Ratio Method
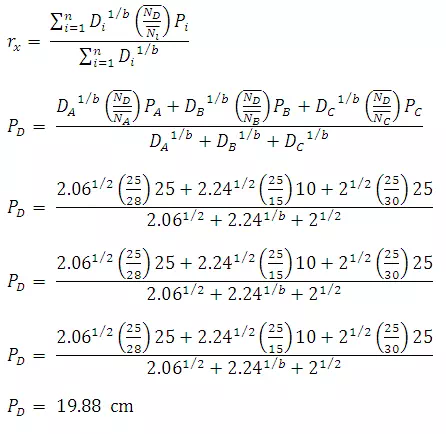
d. Inverse Distance Method