Unit Hydrographs of Different Durations

Lack ofadequate data normally precludes development ofunit hydrographscovering a wide range ofdurations for a given catchment. Undersuch conditions aD hour unit hydrograph is used to develop unit hydrographs of differing durations nD. Two methods are available for this purpose.

 Method of Superposition

If a D-h unit hydrograph is available and it is desired todevelop a unit hydrograph of nDh, where n isan integer, it is easily accomplished by superposing n unit hydrograph with each graph separated from the previous on by D-h.

Example 1

The ordinates of a 6-h unit hydrograph are given

Time	(h)	0	6	12	18	24	30
Ordinate of 6-h UH	(m3/s)	0	20	60	150	120	90
Time	(h)	36	42	48	54	60	66
Ordinate of 6-h UH	(m3/s)	66	50	32	20	10	0

Derive a 12-h unit hydrograph for the catchment.

Answer 

C1	C2	C3	C4= C2+C3	C5 = (C4/(12/6))
Time	Ordinate of 6-h UH	Ordinates of 6-h UH lagged by 6-h		C5 = (C4/2)
				Ordinates of 12-h UH
h	m3/s	m3/s	m3/s	m3/s
0	0		0	0
6	20	0	20	10
12	60	20	80	40
18	150	60	210	105
24	120	150	270	135
30	90	120	210	105
36	66	90	156	78
42	50	66	116	58
48	32	50	82	41
54	20	32	52	26
60	10	20	30	15
66	0	10	10	5
72		0	0	0

S-curve

If it is desired to develop a unit hydrograph of durationmD, where m is a fraction, the method of superposition cannot be used. A different technique known as the S-curve method is adopted in such cases, and this method isapplicable forrational values of m. 

The S-curve, also known as S-hydrograph is a hydrograph produced by a continuous effective rainfall at a constant rate for an infinite period. It is a curve obtained by summation of an infinite series of D-h unit hydrographs spaced D-hapart.

Fig .1 shows such a series of D-hhydrograph arranged with their starting points D-hapart.

 At any given time the ordinates of the various curves occurring at that time coordinate are summed up to obtain ordinates of the S-curve. A smooth curve through these ordinate results in an S-shaped curve called S-curve.

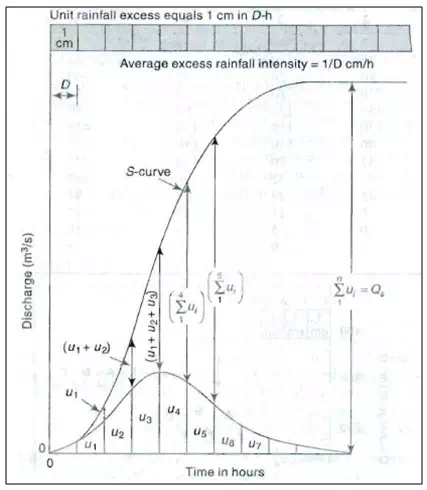
Fig. .1S-curve.

This S-curve is due to a D-h unit hydrograph. It has an initial steep portion and reaches a maximum equilibrium discharge at a time equal to the first unit hydrograph. The average intensity of ER producing the S-curve is 1/D cm/h and the equilibrium discharge,

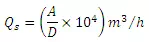
Where A is area of catchment in km2 and D is duration in hours of ER of the unit hydrograph used in deriving the S-curve.

 By definition an S-curve is obtained by adding a string of D-h unit hydrographs each lagged by D-hours from one another. Further, if Tb = base period of the unit hydrograph, addition of only Tb/D unit hydrographs are sufficient to obtain the S-curve. However, an easier procedure based on the basic property of the S-curve is available for the construction of S-curves.

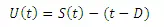
or

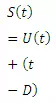 (26.1)

The term S (t-D)could be called S-curve addition at time t

For all

 Example 2

The ordinate of 2-h unit hydrograph of a basin are given:

Time	(h)	0	2	4	6	8	10	12
2-h UH Ordinates	(m3/s)	0	25	100	160	190	170	110
Time	(h)	14	16	18	20	22	24	26
2-h UH Ordinates	(m3/s)	70	30	20	6	0	0	0

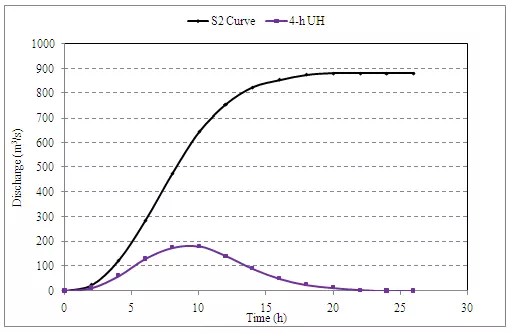
Compute a 4-h unit hydrograph ordinate and plot: (i) the S-curve (ii) the 4-h UG

C1	C2	C3	C4	C5	C6 = C4-C5	C7 = C6/ (4/2)
Time	2-h UH Ordinates	S curve addition	S2 curve ordinate	S2 curve lagged by 4 h	DRH of (4/2)= 2 cm	4-h UH Ordinates
h	m3/s				m3/s	m3/s
0	0	0	0		0	0.0
2	25	0	25		25	12.5
4	100	25	125	0	125	62.5
6	160	125	285	25	260	130.0
8	190	285	475	125	350	175.0
10	170	475	645	285	360	180.0
12	110	645	755	475	280	140.0
14	70	755	825	645	180	90.0
16	30	825	855	755	100	50.0
18	20	855	875	825	50	25.0
20	6	875	881	855	26	13.0
22	0	881	881	875	6	3.0
24	0	881	881	881	0	0.0
26	0	881	881	881	0	0.0