Unit Hydrograph

Definition of Unit Hydrograph

This method was first suggested by Sherman in 1932

· A unit hydrograph is defined as the hydrograph of direct runoff resulting from one unit depth (1 cm) of rainfall excess occurring uniformly over the basin and at a uniform rate for a specified duration (D hours).

· The definition of a unit hydrograph implies the following:

· The unit hydrograph represents the lumped response or the catchment to a limit rainfall excess of D-hduration to produce a direct-runoff hydrograph. It relates only the direct runoff to the rainfall excess. Hence the volume of water contained in the unit hydrograph must be equal to the rainfall excess. As 1 cm depth of rainfall excess is considered the area of the unit hydrograph is equal to a volume given by 1cm over the catchment.

· The rainfall is considered to have an average intensity of excess rainfall (ER) of 1/D cm/h for the duration D-hof the storm.

· The distribution of the storm is considered to be uniform all over the catchment.

Example 1

The ordinates of a hydrograph of surface runoff resulting from 4.5 cm of rainfall excess of duration 8 h in a catchment are as follows:

Time	(h)	0	5	13	21	28	32	35	41
Discharge	(m3/s)	0	40	210	400	600	820	1150	1440
Time	(h)	45	55	61	91	98	115	138
Discharge	(m3/s)	1510	1420	1190	650	520	290	0

Determine the ordinates of the 8-h unit hydrograph for this catchment.

Answer

C1	C2	C3	C4=C2/C3
Time	DRH	Excess Rainfall	8-h UH
h	m3/s	cm	m3/s
0	0	4.5	0.0
5	40	4.5	8.9
13	210	4.5	46.7
21	400	4.5	88.9
28	600	4.5	133.3
32	820	4.5	182.2
35	1150	4.5	255.6
41	1440	4.5	320.0
45	1510	4.5	335.6
55	1420	4.5	315.6
61	1190	4.5	264.4
91	650	4.5	144.4
98	520	4.5	115.6
115	290	4.5	64.4
138	0	4.5	0.0

Assumptions of Unit Hydrograph Theory

1. The effective rainfall is uniformly distributed within its duration or specified period of time.

2. The effective rainfall is uniformly distributed over the whole area of drainage basin

3. The time base of the direct runoff hydrograph, i.e., the duration of the direct runoff hydrograph, depends only on the effective rainfall duration, and is independent of the effective rainfall intensity.

4. The response of the drainage basin is linear. This implies that the principles of proportionality and superpositionare applicable.

5. As per proportionality principle, the DRH ordinates are proportional to the effective rainfall intensity.

Similarly, as per superposition principle, DRH ordinates due to a complex storm, having varying effective rainfall intensities, can be obtained by superimposing the DRH due to each element of effective rainfall in succession.

5. The unit hydrograph reflects the basic effects of various physical characteristics of the basin, which do not change in time. This implies that the principle of time invarianceis valid.

 The definition of the UH together with these assumptions constitutes what is now called the unit hydrograph theory.

 Since in practice, assumption (1) and (2) are never satisfied, these forms the limitations of unit hydrograph theory.

 Unit hydrograph theory can be applied only for a basin having drainage area between 200 ha to 5, 00,000 ha

Uses of Unit Hydrograph

1. Development of flood hydrograph for extreme rainfall magnitudes for use in the design of hydraulic structures.

2. Extension of flood-flow records based on rainfall records.

3. Development of flood forecasting and warning systems based on rainfall.

 Application of Unit Hydrograph

Let it be assumed that a D-hunit-hydrograph and the storm hyetograph are available. The initial losses and infiltration losses arc estimated and deducted from the storm hydrograph to obtain the ERH. The ERH is then divided into M blocks of D-h duration each. The rainfall excess in each D-hduration is then operated upon the unit hydrograph successively to get the various DRH curves. The ordinates of these DRHs are suitably lagged to obtain the proper time sequence and are then collected and added at each time element to obtain the required net DRH due to the storm.

Consider Fig. 1 in which a sequence of M rainfall excess values R1, R2, R3… Rm each of duration D-h duration is shown. The line u[t]is the ordinate of a D-h unit hydrograph at t h from the beginning.

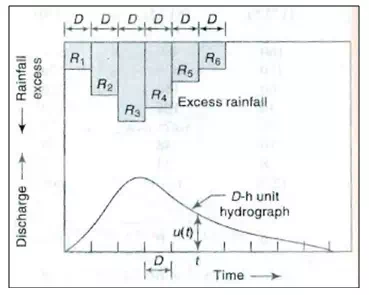
Fig.1.DRH due to an ERH.

The direct runoff' due to R1 at time t is

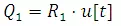
The direct runoff due to R1at time (t -D)is

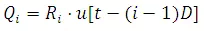
Similarly,

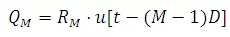
and

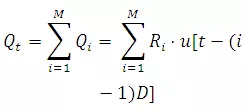
Thus at any time t, the total direct runoff is

After deriving the net DRH, the estimated base flow is then added to obtain the total flood hydrograph.

Example 2

The ordinates of a 6-h unit hydrograph area given:

Time	(h)	0	3	6	9	12	15	18	21
6-h UH Ordinates	(m3/s)	0	150	250	450	600	700	800	750
Time	(h)	24	30	36	42	48	54	60	66
6-h UH Ordinates	(m3/s)	700	600	450	320	200	100	50	0

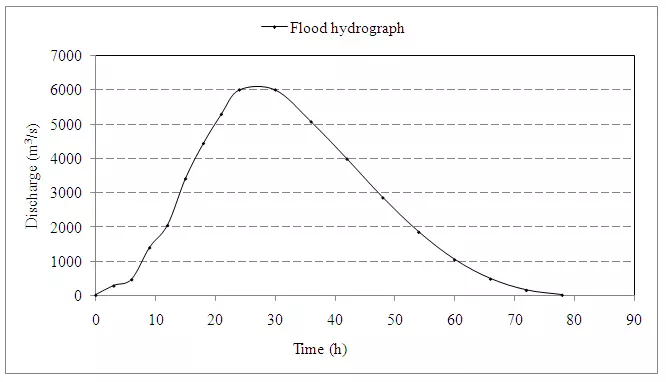
A storm had three successive 6-h intervals of rainfall magnitude of 3.0, 5.0, and 4.0 cm, respectively. Assuming aindex of 0.20 cm/h and base flow of 30 m3/s, determine and plot the resulting hydrograph of flow.

Answer

	(1)	(2)	(3)
Rainfall, (cm)	3	5	4
Ø index, (cm/h)	0.20	0.20	0.20
Time interval ,(h)	6	6	6
losses (Ø * Δt), (cm)	1.2	1.2	1.2
Excess rainfall (Rainfall-Initial losses), (cm)	1.8	3.8	2.8

C1	C2	C3=C2*1.8	C4=C2*3.8	C5=C2*2.8	C6= C3+C4+C5	C7	C8= C7+C6
Time	6-h UH	DRH due to	DRH due to	DRH due to		Base flow	Ordinates of flood
		1.8 cm ER	3.8 cm ER	2.8 cm ER			hydrograph
			lagged by 6-h	lagged by 12-h
h	m3/s	m3/s	m3/s	m3/s	m3/s	m3/s	m3/s
0	0	0			0	30	30
3	150	270			270	30	300
6	250	450	0		450	30	480
9	450	810	570		1380	30	1410
12	600	1080	950	0	2030	30	2060
15	700	1260	1710	420	3390	30	3420
18	800	1440	2280	700	4420	30	4450
21	750	1350	2660	1260	5270	30	5300
24	700	1260	3040	1680	5980	30	6010
30	600	1080	2660	2240	5980	30	6010
36	450	810	2280	1960	5050	30	5080
42	320	576	1710	1680	3966	30	3996
48	200	360	1216	1260	2836	30	2866
54	100	180	760	896	1836	30	1866
60	50	90	380	560	1030	30	1060
66	0	0	190	280	470	30	500
72		0	0	140	140	30	170
78		0	0	0	0	30	30