Channel Characteristics of Watersheds
Number of Channels and their Order
Identification of first-order channels is the first step in applying channel order in hydrology. Application of stream ordering requires the use of a topographic map. Fig 16.5 shows the Strahler method of channel ordering. The number of stream channels of each order is expressed by a mathematical relation, known as Horton's law of channel numbers, in which the number of stream channels of each order forms an inverse geometric sequence with order number,
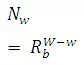 (17.1)
(17.1)
Or
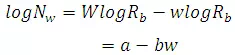 (17.2)
(17.2)
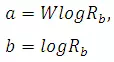 (17.3)
(17.3)
WhereNw = number of streams of order w; W = order of the watershed; andRb = Bifurcation Ratio, defined as Rb = Nw/Nw+1, and varies between 3 and 5. This law is an expression of topological phenomenon, and is a measure of drainage efficiency.
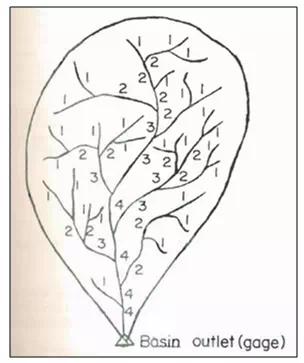
Fig. Channel ordering by the Strahler method.
The number of channels of a given order in a drainage basin is a function of the nature of the surface of that drainage basin. In general, the greater the infiltration of the soil material covering the basin, the fewer will be the number of channels required to carry the remaining runoff water. Moreover, the large number of channels of a given order, the smaller is the area drained by each channel order.
Channel Length
This refers to the length of channels of each order. The average length of channels of each higher order increases as a geometric sequence. Thus, the first-order channels are the shortest of all the channels and the length increases geometrically as the order increases. This relation is called Horton's law of channel lengths and can be formulated as
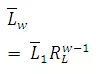 (17.4)
(17.4)
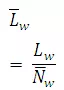 (17.5)
(17.5)
whereLw= total length of all channels of order w; Nw = number of channels of order w; = mean channel length of order w; = mean length of the first-order streams; and RL = Stream-Length Ratio, defined as RL = Lw/Lw-1, and is generally varies between 1.5 and 3.5.
Channel Area
The channel area of order w, Aw, is the area of the watershed that contributes to the channel segment of order w and all lower-order channels. Hack (1957) derived an expression for Aw based on , Rb, and r, which can be written as
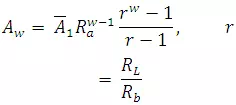 (17.6)
(17.6)
The ratios Rb,RL, and Ra, are of fundamental significance not only for describing drainage-basin composition, but also for hydrologic synthesis.
Channel Profile
The longitudinal channel profile represents the relationship between altitude and horizontal distance, and can be determined from a watershed topographic map. Data on channel profile are used to compute the slope of the channel of a given order. Standard curve-fitting techniques can be used to represent the channel profile mathematically (Strahler, 1964).
The channel profile is normally found to be concave upward. The nature of concavity is a function of the basin geology and precipitation (Hack, 1957). Generally, the upper part of the drainage basin is fairly uniform. Where non-uniform geology occurs in a drainage basin, rocks more resistant to erosion distort the uniform nature of the concave profile. The result of changes in the stream profile caused by bedrock geology can cause large variations in the flow velocity of a stream channel.
Channel Slope
Channel slope has a profound effect on the velocity of flow in a channel, and, consequently, on the flow characteristics of runoff from a drainage basin. The importance of channel slope lies in two areas: (1) determining discharge and velocity using the Manning or Chezy equation, and (2) as a variable in multivariate analysis to determine the amount of influence accounted for by channel slope.
Law of Stream Slopes
Horton (1945) introduced the law of stream slopes, which states that the average slope of streams of each order tends to approximate an inverse geometric series.
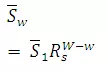 (17.7)
(17.7)
Where 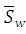 is the average slope of streams
of order w;
is the average slope of streams
of order w; 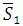 is
the average slope of first-order streams; Rs is the slope ratio defined
as
is
the average slope of first-order streams; Rs is the slope ratio defined
as 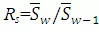 ; and W is the order of the
basin. The value of Rs is approximately 0.55.
; and W is the order of the
basin. The value of Rs is approximately 0.55.
Drainage Density
It is defined as the length of drainage per unit area. This term was first introduced by Horton (1932) and is expressed as
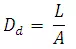
Or
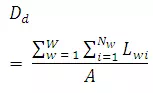 (17.8)
(17.8)
WhereDd is the drainage density of a watershed of order W in kilometers per square kilometer, L is the total length of all channels of all orders in the drainage basin, and A is the area of the drainage basin in square kilometers.Dd is a measure of the closeness (density) of channel spacing. It is an indication of the drainage efficiency of overland flow and the length of overland flow as well as the index of relative proportions.
Constant of Channel Maintenance
Schumm (1956) defined constant of channel maintenance as the inverse of the drainage density. Its value increases with the size of watershed. It provides an estimate of the area in square meters of watershed required to maintain a meter of channel.
Stream Frequency
The number of stream channels per unit area is called the stream frequency.
Length of Overland Flow
As rain falls on a drainage-basin surface, it flows down slope toward a channel. The maximum length of this surface flow is called the length of overland flow.Horton (1945) recommended using one-half the reciprocal of the drainage density to determine the average of overland flow for the entire drainage basin. Because the drainage density is a function of infiltration characteristics of the drainage basin, so, too, must be length of overland flow.
Horton (1945) expressed the length of overland flow Loas
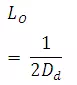 (17.9)
(17.9)