An Application: Convergent-divergent Nozzles

In typical engineering applications, compressible flow typically occurs in ducts, e.g. engine intakes, or through the exhaust nozzles of afterburners and rockets. This latter type of flow typically features changes in area. If we consider a differential, i.e. infinitesimally small control volume, where the cross-sectional area changes by , then the velocity of the flow must also change by a small amount in order to conserve the mass flow rate. Under these conditions we can show that the change in velocity is related to the change in area by the following equation:

$\left( M^2 - 1 \right) \frac{dv}{v} = \frac{dA}{A}$

Without solving this equation for a specific problem we can reveal some interesting properties of compressible flow:

· For M < 1, i.e. subsonic flow, $-c \frac{dv}{v} = \frac{dA}{A}$ with a positive constant. This means that increasing the flow velocity is only possible with a decrease in cross-sectional area and vice versa.

· For M = 1, i.e. sonic flow $0 = \frac{dA}{A}$ . As has to be finite this implies that and therefore the area must be a minimum for sonic flow.

· For M > 1, i.e. supersonic flow $+ c \frac{dv}{v} = \frac{dA}{A}$ . This means that increasing the flow velocity is only possible with an increase in cross-sectional area and vice versa.

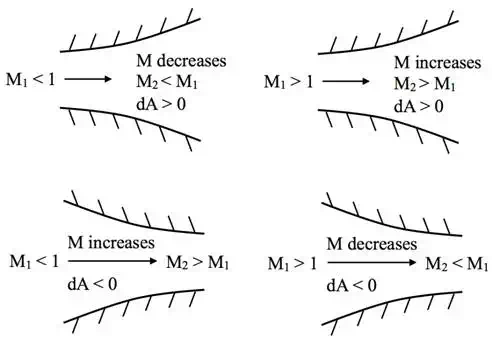
Subsonic and supersonic flow in nozzles

Hence, because of the term , changes in subsonic and supersonic flows are of opposite sign. This means that if we want to expand a gas from subsonic to supersonic speeds, we must first pass the flow through a convergent nozzle to reach Mach 1, and then expand it in a divergent nozzle to reach supersonic speeds. Therefore, at the point of minimum area, known as the throat, the flow must be sonic and, as a result, rocket engines always have large bell-shaped nozzle in order to expand the exhaust gases into supersonic jets.

The flow through such a bell-shaped convergent-divergent nozzle is driven by the pressure difference between the combustion chamber and the nozzle outlet. In the combustion chamber the gas is basically at rest and therefore at stagnation pressure. As it exits the nozzle, the gas is typically moving and therefore at a lower pressure. In order to create supersonic flow, the first important condition is a high enough pressure ratio between the combustion chamber and the throat of the nozzle to guarantee that the flow is sonic at the throat. Without this critical condition at the throat, there can be no supersonic flow in the divergent section of the nozzle.

We can determine this exact pressure ratio for dry air ( $\gamma = 1.4$ ) from the relationship between pressure and Mach number given above:

Therefore, a pressure ratio greater than or equal to 1.893 is required to guarantee sonic flow at the throat. The temperature at this condition would then be:

$\frac{T_t}{T} = 1 + \frac{\gamma-1}{2} 1^2 = 1.2$

or 1.2 times smaller than the temperature in the combustion chamber (as long as there is no heat loss or work done in the meantime, i.e. isentropic flow).

Shock Waves

The term “shock wave” implies a certain sense of drama; the state of shock after a traumatic event, the shock waves of a revolution, the shock waves of an earthquake, thunder, the cracking of a whip, and so on. In aerodynamics, a shock wave describes a thin front of energy, approximately $10^{-7}$ m in thickness (that’s 0.1 microns, or 0.0001 mm) across which the state of the gas changes abruptly. The gas density, temperature and pressure all significantly increase across the shock wave. A specific type of shock wave that lends itself nicely to straightforward analysis is called a normal shock wave, as it forms at right angles to the direction of motion. The conservation laws stated at the beginning of this post still hold and these can be used to prove a number of interesting relations that are known as the Prandtl relation and the Rankine equations.

The Prandtl relation provides a means of calculating the speed of the fluid flow after a normal shock, given the flow speed before the shock.

$V_1 V_2 = \frac{2a_t^2}{\gamma+1}$

where $a_t = \sqrt{\gamma R T_t}$ is the speed of sound at the stagnation temperature of the flow. Because we are assuming no external work or heat transfer across the shock wave, the internal energy of the flow must be conserved across the shock, and therefore the stagnation temperature also does not change across the shock wave. This means that the speed of sound at the stagnation temperature must also be conserved and therefore the Prandtl relation shows that the product of upstream and downstream velocities must always be a constant. Hence, they are inversely proportional.

We can further extend the Prandtl relation to express all flow properties (speed, temperature, pressure and density) in terms of the upstream Mach number , and hence the degree of compressibility before the shock wave. In the Prandtl relation we replace the velocities with their Mach numbers and divide both sides of the equations by

$\frac{a_1 M_1}{a_t} \frac{a_2 M_2}{a_t} = \frac{2}{\gamma+1}$

and because we know the relationship between temperature, stagnation temperature and Mach number from above:

$\frac{a}{a_t} = \sqrt{\frac{T}{T_t}} = \left( 1 + \frac{\gamma-1}{2} M^2 \right)^{-1/2}$

substitution for states 1 and 2 the Prandtl relation is transformed into:

$M_2^2 = \frac{M_1^2 + \frac{2}{\gamma-1}}{\left(\frac{2 \gamma}{\gamma-1}\right) M_1^2 - 1}$

This equation looks a bit clumsy but it is actually quite straightforward given that the terms involving $\gamma$ are constants. For clarity a graphical representation of the the equation is shown below.

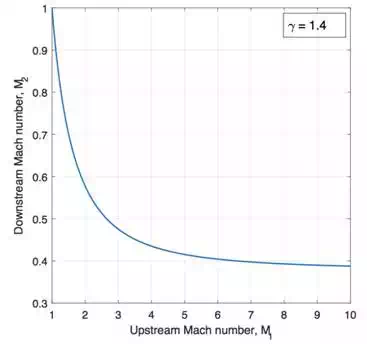
Change in Mach number across a shock wave

It is clear from the figure that for we necessarily have . Therefore a shock wave automatically turns the flow from supersonic to subsonic. In the case of we have reached the limiting case of a sound wave for which there is no change in the gas properties. Similar expressions can also be derived for the pressure, temperature and density, which all increase across a shock wave, and these are known as the Rankine equations.

Both the temperature and pressure ratios increase with higher Mach number such that both and tend to infinity as tends to infinity. The density ratio however, does not tend to infinity but approaches an asymptotic value of 6 as increases. In isentropic flow, the relationship $\frac{p_2}{p_1} = \left(\frac{\rho_2}{\rho_1}\right)^\gamma$ between the pressure ratio and the density ratio $\rho_2 / \rho_1$ must hold. Given that tends to infinity with increasing but $\rho_2$ does not, this implies that the above relation between pressure ratio and density ratio must be broken with increasing , i.e. the flow can no longer conserve entropy. In fact, in the limiting case of a sound wave, where , there is an infinitesimally weak shock wave and the flow is isentropic with no change in the gas properties. When a shock wave forms as a result of supersonic flow the entropy always increases across the shock.

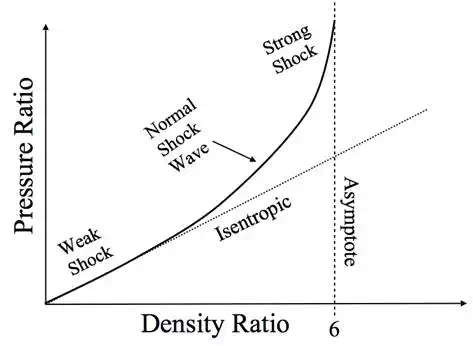
Pressure and density ratios across a shock wave

Even though the Rankine equations are valid mathematically for subsonic flow, the predicted fluid properties lead to a decrease in entropy, which contradicts the Second Law of Thermodynamics. Hence, shock waves can only be created in supersonic flow and the pressure, temperature and density always increase across it.