Supersonic Aerodynamics: Designing Rocket Nozzles

(Caveat: There is a little bit more maths in this post than usual. I have tried to explain the equations as good as possible using diagrams. In any case, the real treat is at the end of the post where I go through the design of rocket nozzles. However, understanding this design methodology is naturally easier by first reading what comes before.)

One of the most basic equations in fluid dynamics is Bernoulli’s equation: the relationship between pressure and velocity in a moving fluid. It is so fundamental to aerodynamics that it is often cited (incorrectly!) when explaining how aircraft wings create lift. The fact is that Bernoulli’s equation is not a fundamental equation of aerodynamics at all, but a particular case of the conservation of energy applied to a fluid of constant density.

The underlying assumption of constant density is only valid for low-speed flows, but does not hold in the case of high-speed flows where the kinetic energy causes changes in the gas’ density. As the speed of a fluid approaches the speed of sound, the properties of the fluid undergo changes that cannot be modelled accurately using Bernoulli’s equation. This type of flow is known as compressible. As a rule of thumb, the demarcation line for compressibility is around 30% the speed of sound, or around 100 m/s for dry air close to Earth’s surface. This means that air flowing over a normal passenger car can be treated as incompressible, whereas the flow over a modern jumbo jet is not.

The fluid dynamics and thermodynamics of compressible flow are described by five fundamental equations, of which Bernoulli’s equation is a special case under the conditions of constant density. For example, let’s consider an arbitrary control volume of fluid and assume that any flow of this fluid is

· adiabatic, meaning there is no heat transfer out of or into the control volume.

· inviscid, meaning no friction is present.

· at constant energy, meaning no external work (for example by a compressor) is done on the fluid.

This type of flow is known as isentropic (constant entropy), and includes fluid flow over aircraft wings, but not fluid flowing through rotating turbines.

At this point you might be wondering how we can possible increase the speed of a gas without passing it through some machine that adds energy to the flow?

The answer is the fundamental law of conservation of energy. The temperature, pressure and density of a fluid at rest are known as the stagnation temperature, stagnation pressure and stagnation density, respectively. These stagnation values are the highest values that the gas can possibly attain. As the flow velocity of a gas increases, the pressure, temperature and density must fall in order to conserve energy, i.e. some of the internal energy of the gas is converted into kinetic energy. Hence, expansion of a gas leads to an increase in its velocity.

The isentropic flow described above is governed by five fundamental conservation equations that are expressed in terms density ( $\rho$ ), pressure (), velocity (), area (), mass flow rate ( $\dot{m}$ ), temperature () and entropy (). This means that at two stations of the flow, 1 and 2, the following expressions must hold:
– Conservation of mass: $\dot{m}_1 = \dot{m}_2 \Rightarrow \rho_1 v_1 A_1 = \rho_2 v_2 A_2$
– Conservation of linear momentum: $\mathrm{d}F = \mathrm{d}m a = \dot{m} \mathrm{d} v \Rightarrow p_1 A_1 - p_2 A_2 = \dot{m} \left( v_2 - v_1\right)$
– Conservation of energy: $T_1 + \frac{v_1^2}{2 c_p} = T_2 + \frac{v_2^2}{2 c_p} = constant$
– Equation of state: $p = \rho R T$
– Conservation of entropy (in adiabatic and inviscid flow only):

where is the specific universal gas constant (normalised by molar mass) and is the specific heat at constant pressure.

The Speed of Sound

Fundamental to the analysis of supersonic flow is the concept of the speed of sound. Without knowledge of the local speed of sound we cannot gauge where we are on the compressibility spectrum.

As a simple mind experiment, consider the plunger in a plastic syringe. The speed of sound describes the speed at which a pressure wave is transmitted through the air chamber by a small movement of the piston. As a very weak wave is being transmitted, the assumptions made above regarding no heat transfer and inviscid flow are valid here, and any variations in the temperature and pressure are small. Under these conditions it can be shown from only the five conservation equations above that the local speed of sound within the fluid is given by:

$a = \sqrt{\gamma R T}$

The term $\gamma$ is the heat capacity ratio, i.e. the ratio of the specific heat at constant pressure () and specific heat at constant volume (), and is independent of temperature and pressure. The specific universal gas constant , as the name suggests, is also a constant and is given by the difference of the specific heats, . As the above equation shows, the speed of sound of a gas only depends on the temperature. The speed of sound in dry air ( J/(kg K), $\gamma$ = 1.4) at the freezing point of 0° C (273 Kelvin) is 331 m/s.

Why is the speed of sound purely a function of temperature?

Well, the temperature of a gas is a measure of the gas’ kinetic energy, which essentially describes how much the individual gas molecules are jiggling about. As the air molecules are moving randomly with differing instantaneous speeds and energies at different points in time, the temperature describes the average kinetic energy of the collection of molecules over a period of time. The higher the temperature the more ferocious the molecules are jiggling about and the more often they bump into each other. A pressure wave momentarily disturbs some particles and this extra energy is transferred through the gas by the collisions of molecules with their neighbours. The higher the temperature, the quicker the pressure wave is propagated through the gas due to the higher rate of collisions.

This visualisation is also helpful in explaining why the speed of sound is a special property in fluid dynamics. One possible source of an externally induced pressure wave is the disturbance of an object moving through the fluid. As the object slices through the air it collides with stationary air particles upstream of the direction of motion. This collision induces a pressure wave which is transmitted via the molecular collisions described above. Now imagine what happens when the object is travelling faster than the speed of sound. This means the moving object is creating new disturbances upstream of its direction of motion at a faster rate than the air can propagate the pressure waves through the gas by means of molecular collisions. The rate of pressure wave creation is faster than the rate of pressure wave transmission. Or put more simply, information is created more quickly than it can be transmitted; we have run out of bandwidth. For this reason, the speed of sound marks an important demarcation line in fluid dynamics which, if exceeded, introduces a number of counter-intuitive effects.

Given the importance of the speed of sound, the relative speed of a body with respect to the local speed of sound is described by the Mach Number:

$M = \frac{v}{a} = \frac{v}{\sqrt{\gamma R T}}$

The Mach number is named after Ernst Mach who conducted many of the first experiments on supersonic flow and captured the first ever photograph of a shock wave (shown below).

As described previously, when an object moves through a gas, the molecules just ahead of the object are pushed out of the way, creating a pressure pulse that propagates in all directions (imagine a spherical pressure wave) at the speed of sound relative to the fluid. Now let’s imagine a loudspeaker emitting three sound pulses at equal intervals, , , .

If the object is stationary, then the three sound pulses at times , and are concentric (see figure below).

However, if the object starts moving in one direction, the centre of the spheres shift to the side and the sound pulses bunch up in the direction of motion and spread out in the opposite direction. A bystander listening to the sound pulses upstream of the loudspeaker would therefore hear a higher pitched sound than a downstream bystander as the frequency the sound waves reaching him are higher. This is known as the Doppler effect.

If the object now accelerates to the local speed of sound, then the centres of the sound pulse spheres will be travelling just as fast as the sound waves themselves and the spherical waves all touch at one point. This means no sound can travel ahead of the loudspeaker and consequently an observer ahead of the loudspeaker will hear nothing.

Finally, if the loudspeaker travels at a uniform speed greater than the speed of sound, then the loudspeaker will in fact overtake the sound pulses it is creating. In this case, the loudspeaker and the leading edges of the sound waves form a locus known as the Mach cone. An observer standing outside this cone is in a zone of silence and is not aware of the sound waves created by the loudspeaker.

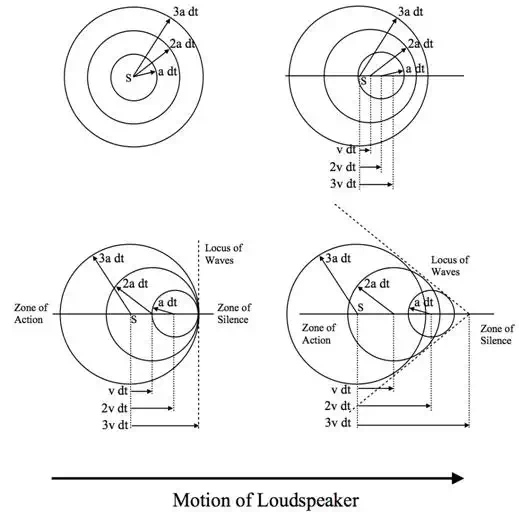
Speed of Sound

S is the starting point of the load speaker which then moves to the right of the screen emitting three sound pulses at times dt, 2dt and 3dt.

The half angle of this cone is known as the Mach angle and is equal to

$\sin \mu = \frac{1}{M}$

and therefore $\mu = 90^\circ$ when the object is travelling at the speed of sound and $\mu$ decreases with increasing velocity.

As mentioned previously, the temperature, pressure and density of the gas all fall as the flow speed of the gas increases. The relation between Mach number and temperature can be derived directly from the conservation of energy (stated above) and is given by:

$\frac{T_t}{T} = 1 + \frac{\gamma-1}{2} M^2$

where is the maximum total temperature, also known as stagnation temperature, and is called the static temperature of the gas moving at velocity .

An intuitive way of explaining the relationship between temperature and flow speed is to return to the description of the vibrating gas molecules. Previously we established that the temperature of a gas is a measure of the kinetic energy of the vibrating molecules. Hence, the stagnation temperature is the kinetic energy of the random motion of the air molecules in a stationary gas. However, if the gas is moving in a certain direction at speed then there will be a real net movement of the air molecules. The molecules will still be vibrating about, but at a net movement in a specific direction. If the total energy of the gas is to remain constant (no external work), some of the kinetic energy of the random vibrations must be converted into kinetic energy of directed motion, and hence the energy associated with random vibration, i.e. the temperature, must fall. Therefore, the gas temperature falls as some of the thermal internal energy is converted into kinetic energy.

In a similar fashion, for flow at constant entropy, both the pressure and density of the fluid can be quantified by the Mach number.

$\frac{p_t}{p} = \left( 1 + \frac{\gamma-1}{2} M^2\right)^{\frac{\gamma}{\gamma-1}}$
$\frac{\rho_t}{\rho} = \left( 1 + \frac{\gamma-1}{2} M^2\right)^{\frac{1}{\gamma-1}}$

In this regard the Mach number can simply be interpreted as the degree of compressibility of a gas. For small Mach numbers (M< 0.3), the density changes by less than 5% and this is why the assumptions of constant density underlying Bernoulli’s equation are applicable.