The History of Rocket Science

Rocket technology has evolved for more than 2000 years. Today’s rockets are a product of a long tradition of ingenuity and experimentation, and combine technical expertise from a wide array of engineering disciplines. Very few, if any, of humanity’s inventions are designed to withstand equally extreme conditions. Rockets are subjected to awesome g-forces at lift-off, and experience extreme hot spots in places where aerodynamic friction acts most strongly, and extreme cold due to liquid hydrogen/oxygen at cryogenic temperatures. Operating a rocket is a balance act, and the line between a successful launch and catastrophic blow-out is often razor thin. No other engineering system rivals the complexity and hierarchy of technologies that need to interface seamlessly to guarantee sustained operation. It is no coincidence that “rocket science” is the quintessential cliché to describe the mind-blowingly complicated.

Fortunately for us, we live in a time where rocketry is undergoing another golden period. Commercial rocket companies like SpaceX and Blue Origin are breathing fresh air into an industry that has traditionally been dominated by government-funded space programs. But even the incumbent companies are not resting on their laurels, and are developing new powerful rockets for deep-space exploration and missions to Mars. Recent blockbuster movies such as Gravity, Interstellar and The Martian are an indication that space adventures are once again stirring the imagination of the public.

What better time than now to look back at the past 2000 years of rocketry, investigate where past innovation has taken us and look ahead to what is on the horizon? It’s certainly impossible to cover all of the 51 influential rockets in the chart below but I will try my best to provide a broad brush stroke of the early beginnings in China to the Space Race and beyond.

The history of rocketry can be loosely split into two eras. First, early pre-scientific tinkering and second, the post-Enlightenment scientific approach. The underlying principle of rocket propulsion has largely remained the same, whereas the detailed means of operation and our approach to developing rocketry has changed a great deal.

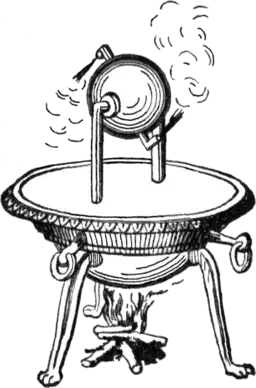
An illustration of Hero’s aeolipile

The fundamental principle of rocket propulsion, spewing hot gases through a nozzle to induce motion in the opposite direction, is nicely illustrated by two historic examples. The Roman writer Aulus Gellius tells a story of Archytas, who, sometime around 400 BC, built a flying pigeon out of wood. The pigeon was held aloft by a jet of steam or compressed air escaping through a nozzle. Three centuries later, Hero of Alexandria invented the aeolipile based on the same principle of using escaping steam as a propulsive fluid. In the aeolipile, a hollow sphere was connected to a water bath via tubing, which also served as a primitive type of bearing, suspending the sphere in mid-air. A fire beneath the water basin created steam which was subsequently forced to flow into the sphere via the connected tubing. The only way for the gas to escape was through two L-shaped outlets pointing in opposite directions. The escaping steam induced a moment about the hinged support effectively rotating the sphere about its axis.

In both these examples, the motion of the device is governed by the conservation of momentum. When the rocket and internal gases are moving as one unit, the overall momentum, the product of mass and velocity, is equal to . Thus for a total mass of rocket and gas, , moving at velocity

$mv = \left(m_r + m_g\right)v = P_1$

As the gases are expelled through the rear of the rocket, the overall momentum of the rocket and fuel has to remain constant as long as no external forces are acting on the system. Thus, if a very small amount of gas $\mathrm{d}m$ is expelled at velocity relative to the rocket (either in the direction of or in the opposite direction), the overall momentum of the system is

$\left(m - \mathrm{d}m\right) \left(v+\mathrm{d}v_r\right) + \mathrm{d}m \left(v + v_e\right) = P_2$

As has to equal to conserve momentum

$mv = \left(m - \mathrm{d}m\right) \left(v+\mathrm{d}v_r\right) + \mathrm{d}m \left(v + v_e\right)$

and by isolating the change in rocket velocity $\mathrm{d}v_r$

$\left(m-\mathrm{d}m\right) \mathrm{d}v_r = -v_e\mathrm{d}m$
$\therefore dv_r = -\frac{\mathrm{d}m}{\left(m-\mathrm{d}m\right)} v_e$

The negative sign in the equation above indicates that the rocket always changes velocity in the opposite direction of the expelled gas. Hence, if the gas is expelled in the opposite direction of the motion (i.e. is negative), then the change in the rocket velocity will be positive (i.e. it will accelerate).

At any time the quantity $M = m-\mathrm{d}m$ is equal to the residual mass of the rocket (dry mass + propellant) and $\mathrm{d}m = \mathrm{d}M$ denotes it change. If we assume that the expelled velocity of the gas remains constant throughout, we can easily integrate the above expression to find the incremental change in velocity as the total rocket mass (dry mass + propellant) changes from an intial mass to a final mass . Hence,

This equation is known as the Tsiolkovsky rocket equation (more on him later) and is applicable to any body that accelerates by expelling part of its mass at a specific velocity.

Often, we are more interested in the thrust created by the rocket and its associated acceleration . Hence, by dividing the equation for by a small time increment

$a_r = \frac{\mathrm{d}v_r}{\mathrm{d}t} = - \frac{\mathrm{d}M}{\mathrm{d}t} \frac{v_e}{M} = \frac{\dot{M}}{M} v_e$

and the associated thrust acting on the rocket is

$F_r = Ma_r = \dot{M} v_e$

where $\dot{M}$ is the mass flow rate of gas exiting the rocket. This simple equation captures the fundamental physics of rocket propulsion. A rocket creates thrust either by expelling more of its mass at a higher rate ( $\dot{M}$ ) or by increasing the velocity at which the mass is expelled. In the ideal case that’s it! (So by idealised we mean constant and no external forces, e.g. aerodynamic drag in the atmosphere or gravity. In actual calculations of the required propellant mass these forces and other efficiency reducing factors have to be included.)

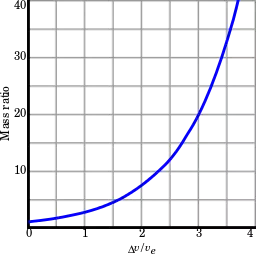
A plot of the rocket equation highlights one of the most pernicious conundrums of rocketry: The amount of fuel required (i.e. the mass ratio ) to accelerate the rocket through a velocity change $\Delta v$ at a fixed effective escape velocity increases exponentially as we increase the demand for greater $\Delta v$ . As the cost of a rocket is closely related to its mass, this explains why it is so expensive to propel anything of meaningful size into orbit ( $\Delta v \approx$ 28,800 km/hr (18,000 mph) for low-earth orbit).

The exponential increase of fuel mass required to accelerate a rocket through a specific velocity change