Flight dynamics - Detail

Flight dynamics is the science of air and space vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of mass, known as pitch, roll and yaw (quite different from their use as Tait-Bryan angles).

Aerospace engineers develop control systems for a vehicle's orientation (attitude) about its center of mass. The control systems include actuators, which exert forces in various directions, and generate rotational forces or moments about the aerodynamic center of the aircraft, and thus rotate the aircraft in pitch, roll, or yaw. For example, a pitching moment is a vertical force applied at a distance forward or aft from the aerodynamic center of the aircraft, causing the aircraft to pitch up or down.

Roll, pitch and yaw refer to rotations about the respective axes starting from a defined equilibrium state. The equilibrium roll angle is known as wings level or zero bank angle, equivalent to a level heeling angle on a ship. Yaw is known as 'heading'. The equilibrium pitch angle in submarine and airship parlance is known as 'trim', but in aircraft, this usually refers to angle of attack, rather than orientation. However, common usage ignores this distinction between equilibrium and dynamic cases.

The most common aeronautical convention defines the roll as acting about the longitudinal axis, positive with the starboard(right) wing down. The yaw is about the vertical body axis, positive with the nose to starboard. Pitch is about an axis perpendicular to the longitudinal plane of symmetry, positive nose up.

A fixed-wing aircraft increases or decreases the lift generated by the wings when it pitches nose up or down by increasing or decreasing the angle of attack (AOA). The roll angle is also known as bank angle on a fixed wing aircraft, which usually "banks" to change the horizontal direction of flight. An aircraft is usually streamlined from nose to tail to reduce drag making it typically advantageous to keep the sideslip angle near zero, though there are instances when an aircraft may be deliberately "sideslipped" for example a slip in a fixed wing aircraft.

Coordinate systems

The position (and hence motion) of an aircraft is generally defined relative to one of 3 sets of co-ordinate systems:

● Wind Axes

● X Axis - Positive in the direction of the oncoming air (relative wind)

● Y Axis - Positive to Right of X Axis, perpendicular to X Axis

● Z Axis - Positive downwards, perpendicular to X-Y plane

● Inertial Axes (or Body Axes) - based about aircraft CG

● X Axis - Positive forward, through nose of aircraft

● Y Axis - Positive to Right of X Axis, perpendicular to X Axis

● Z Axis - Positive downwards, perpendicular to X-Y plane

● Earth Axes

● X Axis - Positive in the direction of North

● Y Axis - Positive in the direction of East (perpendicular to X Axis)

● Z Axis - Positive towards the centre of Earth (perpendicular to X-Y Plane)

For flight dynamics applications the Earth Axes are generally of minimal use, and hence will be ignored. The motions relevant to dynamic stability are usually too short in duration for the motion of the Earth itself to be considered relevant for aircraft.

In flight dynamics, pitch, roll and yaw angles measure both the absolute attitude angles (relative to the horizon/North) and changes in attitude angles, relative to the equilibrium orientation of the vehicle. These are defined as:

● Pitch - Angle of X Body Axis (nose) relative to horizon. Also a positive (nose up) rotation about Y Body Axis

● Roll - Angle of Y Body Axis (wing) relative to horizon. Also a positive (right wing down) rotation about X Body Axis

● Yaw - Angle of X Body Axis (nose) relative to North. Also a positive (nose right) rotation about Z Body axis

In analysing the dynamics, we are concerned both with rotation and translation of this axis set with respect to a fixed inertial frame. For all practical purposes a local Earth axis set is used, this has X and Y axis in the local horizontal plane, usually with the x-axis coinciding with the projection of the velocity vector at the start of the motion, on to this plane. The z axis is vertical, pointing generally towards the Earth's centre, completing an orthogonal set.

In general, the body axes are not aligned with the Earth axes. The body orientation may be defined by three Euler angles, the Tait-Bryan rotations, a quaternion, or a direction cosine matrix (rotation matrix). A rotation matrix is particularly convenient for converting velocity, force, angular velocity, and torque vectors between body and Earth coordinate frames.

Body axes tend to be used with missile and rocket configurations. Aircraft stability uses wind axes in which the x-axis points along the velocity vector. For straight and level flight this is found from body axes by rotating nose down through the angle of attack.

Stability deals with small perturbations in angular displacements about the orientation at the start of the motion. This consists of two components; rotation about each axis, and angular displacements due change in orientation of each axis. The latter term is of second order for the purpose of stability analysis, and is ignored.

Design cases

In analysing the stability of an aircraft, it is usual to consider perturbations about a nominal equilibrium position. So the analysis would be applied, for example, assuming:

Steady level flight

Turn at constant speed

Approach and landing

Take off

The speed, height and trim angle of attack are different for each flight condition, in addition, the aircraft will be configured differently, e.g. at low speed flaps may be deployed and the undercarriage may be down.

Except for asymmetric designs (or symmetric designs at significant sideslip), the longitudinal equations of motion (involving pitch and lift forces) may be treated independently of the lateral motion (involving roll and yaw).

The following considers perturbations about a nominal straight and level flight path.

To keep the analysis (relatively) simple, the control surfaces are assumed fixed throughout the motion, this is stick-fixed stability. Stick-free analysis requires the further complication of taking the motion of the control surfaces into account.

Furthermore, the flight is assumed to take place in still air, and the aircraft is treated as a rigid body.

Spacecraft

Unless designed to conduct part of the mission within a planetary atmosphere, a spacecraft would generally have no discernible front or side, and no bottom unless designed to land on a surface, so reference to a 'nose' or 'wing' or even 'down' is arbitrary. On a manned spacecraft, the axes must be oriented relative to the pilot's physical orientation at the flight control station. Unmanned spacecraft may need to maintain orientation of solar cells toward the Sun, antennas toward the Earth, or cameras toward a target, so the axes will typically be chosen relative to these functions.

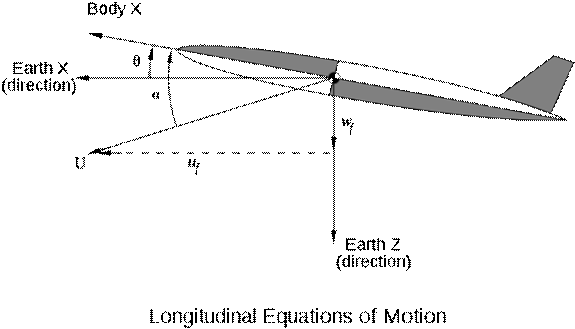
Longitudinal modes

It is common practice to derive a fourth order characteristic equation to describe the longitudinal motion, and then factorise it approximately into a high frequency mode and a low frequency mode. This requires a level of algebraic manipulation which most readers will doubtless find tedious, and adds little to the understanding of aircraft dynamics. The approach adopted here is to use our qualitative knowledge of aircraft behaviour to simplify the equations from the outset, reaching the same result by a more accessible route.

The two longitudinal motions (modes) are called the short period pitch oscillation (SSPO), and the phugoid.

Short-period pitch oscillation

A short input (in control systems terminology an impulse) in pitch (generally via the elevator in a standard configuration fixed wing aircraft) will generally lead to overshoots about the trimmed condition. The transition is characterised by a damped simple harmonic motion about the new trim. There is very little change in the trajectory over the time it takes for the oscillation to damp out.

Generally this oscillation is high frequency (hence short period) and is damped over a period of a few seconds. A real-world example would involve a pilot selecting a new climb attitude, for example 5º nose up from the original attitude. A short, sharp pull back on the control column may be used, and will generally lead to oscillations about the new trim condition. If the oscillations are poorly damped the aircraft will take a long period of time to settle at the new condition, potentially leading to Pilot-induced oscillation. If the short period mode is unstable it will generally be impossible for the pilot to safely control the aircraft for any period of time.

This damped harmonic motion is called the short period pitch oscillation, it arises from the tendency of a stable aircraft to point in the general direction of flight. It is very similar in nature to the weathercock mode of missile or rocket configurations. The motion involves mainly the pitch attitude θ (theta) and incidence α (alpha). The direction of the velocity