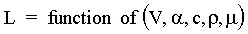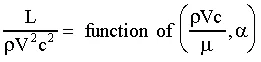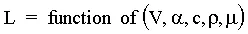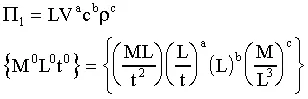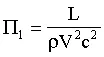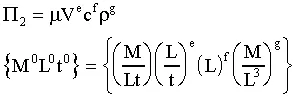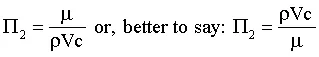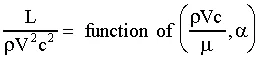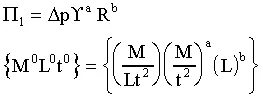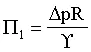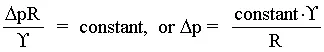Dimensional Analysis and Similarity
Introduction - The Purposes and Usefulness of Dimensional Analysis
- Dimensional analysis is a very powerful tool, not just in fluid mechanics, but in many disciplines. It provides a way to plan and carry out experiments, and enables one to scale up results from model to prototype. Consider, for example, the design of an airplane wing.
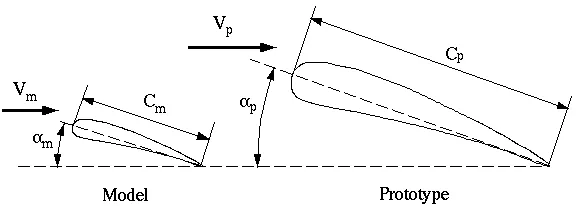
The full-size wing, or prototype, has some chord length, cp, operates at speed Vp, and generates a lift force, Lp, which varies with angle of attack. In addition, the fluid properties of importance to this flow are the density and viscosity. After the preliminary design, it is usually necessary to perform experiments to verify and fine-tune the design. To save both time and money, these tests are usually conducted with a smaller scale model in a wind tunnel or water tunnel. In the sketch above, a geometrically similar model is constructed. In this case, the model is smaller than the prototype. In some cases the opposite is true; i.e. it may be prudent to build a large model of some small prototype in order to perform more accurate experimental analysis.
- The goal of the experimental tests is to find a relationship between the dependent variable (in this case the wing's lift) and the independent variables in the problem (in this case the velocity, the wing's angle of attack, chord length, and the density and viscosity of the fluid). Note that here we are neglecting the speed of sound, which is only important at very high speeds. The functional relationship can be stated as follows:
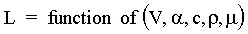
- There is a wrong way and a right way to conduct the experiments. The wrong way is to try to analyze the dependence of lift on each of the five independent variables separately. In other words, run the tests at many velocities (to see the effect of velocity on lift), and many angles of attack (to see the effect of angle of attack on lift), with many different model sizes (to see the effect of chord length on lift), and in many different fluids (to see the effect of viscosity and density on lift). This would take an enormous amount of time and resources, and it would be very difficult to summarize the results succinctly.
- The right way to do the experiments is to first perform a dimensional analysis of the above functional relationship, which leads to a revised form of the relationship in terms of nondimensional parameters or nondimensional groups. In this particular problem, dimensional analysis yields
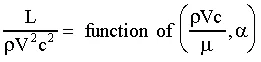
which is much simpler than the original functional relationship. In particular, instead of a dependent variable as a function of five independent variables, the problem has been reduced to one dependent parameter as a function of only two independent parameters. Furthermore, each of these three parameters is dimensionless, which makes them completely independent of the unit system used in the measurements.
- The parameter on the left is a kind of lift coefficient (the actual lift coefficient has a factor of 2 thrown in for convenience), while the first independent parameter on the right is called the Reynolds number. Angle of attack is already dimensionless, so it is a dimensionless group by itself.
- One plot is enough to completely describe the above functional relationship. In particular, lift coefficient is plotted versus angle of attack, and several curves are plotted at constant Reynolds number. This single plot is then valid for any size wing, in any Newtonian incompressible fluid, and at any speed. When experiments are conducted after performing the dimensional analysis, it is realized that only one wind tunnel model needs to be made, and only one fluid needs to be used (that fluid can be air or water or any other Newtonian incompressible fluid)! The wind tunnel or water tunnel test needs to consist of simply measuring lift as a function of velocity and angle of attack. Results of the experiment are plotted nondimensionally as indicated above.
Dynamic Similarity
- The principle of dynamic similarity can be stated as follows:
If the model and prototype are geometrically similar (i.e. the model is a perfect scale replica of the prototype), and if each independent dimensionless parameter for the model is equal to the corresponding independent dimensionless parameter of the prototype, then the dependent dimensionless parameter for the prototype will be equal to the corresponding dependent dimensionless parameter for the model.
- Consider the airplane wing example above. In this case, the two independent dimensionless parameters (those on the right hand side) are Reynolds number and angle of attack. The dependent parameter is the lift coefficient. The model wing in the wind tunnel must obviously be set at the same angle of attack as the desired angle of attack of the prototype. In order to achieve dynamic similarity, the Reynolds number of the model must also equal that of the prototype. Then, dynamic similarity assures us that the lift coefficient of the prototype will equal that of the model. Mathematically, we can solve for the wind tunnel velocity, Vm, required to match Reynolds number, and we can scale up the lift measurement from the wind tunnel tests to the full scale prototype as follows:

In this manner, we can set the wind tunnel speed properly to match Reynolds number. Then, after measuring the lift on the model wing, Lm, we can properly scale (using the last equation above) to predict the lift, Lp, on the prototype.
The Buckingham Pi Technique
- The Buckingham Pi technique is a formal "cookbook" recipe for determining the dimensionless parameters formed by a list of variables. There are six steps, which are outlined below, followed by a couple of example problems. Other examples can be found in the textbook and homework problems.
- Step 1. All the variables are listed and counted - The total number of variables is assigned to variable n. Note: The dependent variable as well as all the independent variables must be included in n, even if they are dimensionless (angles, for example, are already dimensionless, but still get counted in this first step).
- Step 2. The primary dimensions of each of the n variables are listed. As discussed in the text, either the force-length-time-temperature set or the mass-length-time-temperature set of primary dimensions can be used. In this course, only the latter will be used. Table 5.1 in the text provides the dimensions of most of the variables needed in fluid mechanics, and is useful in this step.
- Step 3. The number of repeating variables, j, is found, where j is usually the number of primary dimensions represented in the problem. There are more formal mathematical ways to find j, but in most problems it is sufficient to simply count the number of primary dimensions available from all the original variables. For example, if mass, length, and time each appear in at least one variable, j is set to 3. As the Buckingham Pi technique progresses, it sometimes becomes clear that things just are not working out. In such cases, j should be reduced by 1 and Steps 4 through 6 should be repeated. Once j is found, the number of dimensionless parameters (or "Pi" groups) expected is k = n - j, where k is the number of Pi groups. This equation relating k to n and j is part of the Buckingham Pi Theorem.
- Step 4. A total of j "repeating variables" are chosen, which will be used to generate the Pi groups. It is somewhat arbitrary which variables to pick here, especially when n is large. The main thing that should be kept in mind is that these repeating variables may appear in each of the Pi groups. Therefore, it is important which variables are chosen. Some rules are helpful:
- The dependent variable should not be picked as a repeating variable. Otherwise, it will appear in more than one Pi, which will lead to an implicit expression in Step 6 below.
- The repeating variables must not be able to form a Pi group all by themselves. Otherwise, the procedure in Step 5 will be fruitless.
- Each of the primary dimensions in the problem must be represented. For example, if mass, length, and time appear in the original n variables, these three primary dimensions must also each appear at least once in the repeating variables.
- Variables which are already dimensionless (such as angles) should not be picked. Such variables are already dimensionless Pi groups, and cannot contribute to formulating the remaining Pi groups.
- Two variables with the same dimensions or with dimensions differing by only an exponent should never be picked. For example, if some area and some length are among the list of variables, the length should be chosen as a repeating variable. It would be incorrect to also select the area as a repeating variable, since its dimensions are simply the square of the length, and can contribute nothing additional to the formulation of the Pi groups.
- Variables with very basic dimensions and/or variables that are "common" should be picked as repeating variables. This is perhaps the most difficult aspect of dimensional analysis, especially for the beginning student. After much practice, it becomes more or less obvious which variables to pick. For example, if there is a length, that length should be picked as a repeating variable since it is very basic and desirable in the Pi groups. Likewise, some velocity, mass, time, or density are also good choices. In most fluid flow problems, other flow properties like viscosity or surface tension should not be chosen if there are also more "basic" variables to choose from, such as a length, velocity, time, mass, or density. Why? Because it is usually not desirable to have viscosity or surface tension appear in each of the Pi groups.
- Step 5. The Pi groups are formulated by multiplying each of the remaining variables (those that were not chosen as repeating variables) in turn by the repeating variables, each in turn raised to some unknown exponent. The exponents are found algebraically by forcing the Pi to be dimensionless. The convention is to form the first Pi using the dependent variable. Note that Pi groups can be "adjusted" after they are formed in order to agree with the dimensionless groups commonly used in the literature. For example, a Pi can be raised to any exponent, including -1 which yields the inverse of the Pi. Also, the Pi group can be multiplied by any dimensionless constant without altering its dimensions. (Often, factors of 2 or 1/2 are included in the standard Pi groups.) Table 5.2 in the text lists many of the common dimensionless groups used in Fluid Mechanics. The Pi groups generated in this step should be adjusted, if necessary, and named according to this table.
- Step 6. The Pi groups are written in final functional form, typically as the first Pi as a function of the remaining Pi groups. If only one Pi is found, it must be a constant, since it is a function of nothing else.
Example: Lift on a wing in incompressible flow
Consider the case of incompressible flow over an airplane wing, as discussed in the previous lecture. Wing lift is known to depend on flow speed, angle of attack, chord length of the wing, and density and viscosity of the fluid. Let's examine this problem with the Buckingham Pi technique of dimensional analysis, following the steps outlined above:
- Step 1. n = number of variables in the problem, which is 6 here. n = 6.
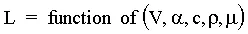
- Step 2. List dimensions of each variable:
Variable | Description | Dimensions |
L | lift force | M(L)(t-2) |
V | velocity | L(t-1) |
c | chord length | L |

| density | M(L-3) |

| viscosity | M(L-1)(t-1) |
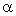
| angle of attack | 1 (dimensionless) |
- Step 3. Find j. Here, try first setting j = number of primary dimensions in the problem. From the above table, mass, length, and time are the only primary dimensions represented by the set of original variables. Thus, set j = 3. This yields k = n - j = 6 - 3 = 3. I.e., we expect three Pi's from the dimensional analysis.
- Step 4. Choose j repeating variables. Here we need to pick 3 repeating variables. Lift force is not a good choice since it is the dependent variable in our problem setup. Angle of attack is not allowed since it is already dimensionless. (Note that angle of attack will be shown to be a dimensionless Pi all by itself!) Out of the remaining four, viscosity is the least "basic" or "desirable" variable to be repeated in all the Pi groups. The best choice here is thus density, velocity, and chord length.
- Step 5. Construct the Pi groups. Let's pick the lift force first since it is the dependent variable:
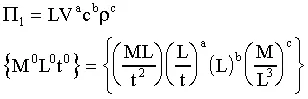
Equating exponents of mass: 0 = 1 + c, or c = -1.
Equating exponents of time: 0 = -2 - a, or a = -2.
Equating exponents of length: 0 = 1 + a + b -3c, or b = -2.
Thus,
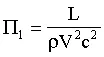
Likewise, construct the second Pi group using viscosity and the repeating variables:
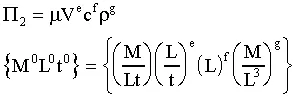
Equating exponents of mass: 0 = 1 + g, or g = -1.
Equating exponents of time: 0 = -1 - e, or e = -1.
Equating exponents of length: 0 = -1 + e + f -3g, or f = -1.
Thus,
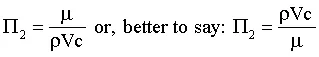
Note that this Pi group has been inverted in order to match the most well known dimensionless group in Fluid Mechanics, the Reynolds number. It would not be mathematically incorrect to leave it "upside down," but it is, shall we say, not "socially acceptable" to do so.
- Step 6. Write the final functional relationship:
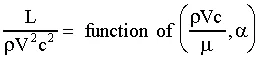
Notice that instead of a dependent variable as a function of five independent variables, the problem has been reduced to one dependent parameter as a function of only two independent parameters. The dependent Pi group on the left hand side is a lift coefficient (which normally has a factor of 2 thrown in for convenience), while the first independent parameter on the right is the Reynolds number, as discussed above.
- Recall the principle of dynamic similarity. In this example, if a geometrically scaled model wing is built, and that wing is tested at some angle of attack and at some Reynolds number, the measured lift coefficient is guaranteed to equal that of the full-scale prototype if operated at the same Reynolds number and the same angle of attack. This is the case even if vastly different fluids are used (air and water for example).
Example: Dimensional analysis of a soap bubble
Consider a soap bubble. It is known that the pressure inside the bubble must be greater than that outside, and that surface tension acts like a "skin" to support this pressure difference. The pressure difference is then a function of surface tension and bubble radius. No other variables are important in this problem. Let's examine this problem with the Buckingham Pi technique of dimensional analysis, following the steps outlined above:
- Step 1. n = number of variables in the problem, which is 3 here. n = 3.

- Step 2. List dimensions of each variable:
Variable | Description | Dimensions |
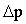
| pressure difference | M(L-1)(t-2) |
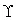
| surface tension | M(t-2) |
R | bubble radius | L |
- Step 3. Find j. Here, try first setting j = number of primary dimensions in the problem. From the above table, mass, length, and time are the only primary dimensions represented by the set of original variables. Thus, set j = 3. This yields k = n - j = 3 - 3 = 0. I.e., we expect zero Pi's from the dimensional analysis. This makes no sense. When this happens, one of two reasons exists: either we don't have enough variables in the original problem statement (not enough physics is represented by the list of variables), or j is wrong. Here, the latter is the case, and we must reduce j by 1 before continuing. Set j = 2, which yields k = n - j = 3 - 2 = 1. I.e., we expect one Pi from the dimensional analysis.
- Step 4. Choose j repeating variables. Here we need to pick 2 repeating variables. Pressure difference is not a good choice since it is the dependent variable in our problem setup. The best choice here is thus surface tension and bubble radius.
- Step 5. Construct the Pi groups. Here there is only one, and it is found by combining the remaining variable with the two repeating variables to form a Pi group, as follows:
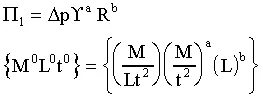
Equating exponents of mass: 0 = 1 + a, or a = -1.
Equating exponents of time: 0 = -1 + b, or b = 1.
Equating exponents of length: 0 = -2 -2a, or a = -1.
Fortunately here, the first and third equation yield the same value of exponent a. If they did not, we would suspect either an algebra mistake or a non-physical setup of the problem. Our result is:
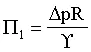
- Step 6. Write the final functional relationship:
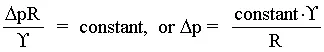
Notice that instead of a dependent variable as a function of two independent variables, the problem has been reduced to one dependent parameter as a function of nothing. In cases like this where there is only one Pi group, that Pi must be a constant. (If it is not a function of anything else, it must be a constant!)
- This is an excellent example of the power of dimensional analysis. Here we have obtained a functional relationship between pressure, radius, and surface tension to within a constant of proportionality without knowing any physics about the problem! Dimensional analysis cannot provide the constant, but it can provide information about how one variable depends on others. For example, our result shows that if the bubble radius is reduced by a factor of 2, the pressure difference will increase by a factor of 2. It also shows that pressure difference is linearly proportional to surface tension. Exact analysis (see Chapter 1 in the text) provides the constant of proportionality in the above expression, namely 4.