Wind tunnel measurements
  

pressure distribution

This  is  used  for  studying  pressure  distribution  across various  models such as Airfoil,  cylinder, special  purpose  shapes . It contains 13 Nos. Of tubes mounted on board with adjustable inclination. Bottom  of  all  tubes  are  interconnected  and in turn  to  the  balancing  reservoir  filled  with  coloured  water . While  the  last  tube  is  left  open  to atmosphere  for  reference ,  all  other 12 tubes  are  connected  at  their  top  to pipe / tube  bundles  of  the  model.  The  required  model  is  held  in  the  test  section   between  holes  provided  front and  back  side   Perspex  windows. The  pressure  tapings  ( tube  outlets )  are  connected  to  the  glass  limbs  of  the  respective  Serial  Number . The  required  degree  of  angle  of  inclination  can  be  given  to the  tube  bundle  and  angle  measured  with  respect  to  the  horizontal .

The coefficient of pressure is obtained by 

velocity measurement. Pitot probe

One very important use of wind tunnels is to visualize flow patterns and measure the pressure at a selected point in the flow field and compute the corresponding speed of air. The equation relates the speed of the fluid at a point to both the mass density of the fluid and the pressures at the same point in the flow field. For steady flow of an incompressible fluid for which viscosity can be neglected, the fundamental equation has the form

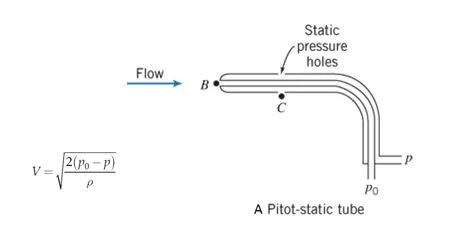
Where V is the speed of the fluid, P0 is the total, also called the stagnation, pressure at that point of measurement, and p is the static pressure at the same point. This equation comes from the application of Bernoulli’s equation for the steady flow of an incompressible and inviscid fluid along a streamline. Bernoulli’s equation is typically obtained by integrating Euler’s equations along a streamline. It will be recalled that Euler’s equations are a special case of the Navier -Stokes equations, when the viscosity of the fluid has been neglected. The Navier-Stokes equations, in turn, are obtained from Newton’s second law when it is applied to a fluid for which the shear deformation follows Newton’s law of viscosity

force coefficients from pressure distribution

By integration the surface pressure coefficient distribution, one can obtain the lift, pressure drag, and pitchining moment coefficients. The lift force is the force acting on the airfoil section perpendicular to the mean flow direction. The pitch moment is the moment about the quarter chord point, positive when nose up. We measure aerodynamic quantities in the middle of the airfoil section and assume that the flow is approximately two-dimensional. In this special case it is convenient to look at the force and moment per unit span. The section lift, pressure drag and moment coefficients are respectively defined as 

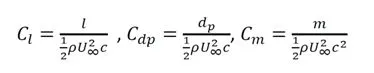
With L the lift force per unit span, dp the drag force per unit span and m the pitch moment per unit span and c is the chord length.

  forces from strain gauge load cells

a)         WIND TUNNEL  BALANCE :

The  tunnel  balance is  three component  type  (  three forces )  designed  using  the electrical  strain  gauges  to indicate  separately  on the  digital  indicator. The balance is intended for indicating the lift , drag & side force in case of airfoils, and drag force only in case of bluff bodies,Viz., spherical, Hemi - spherical, Flat disc. These models are mounted on the string (Vertical square rod) situated exactly beneath the test section. The output from the lift, drag & side forces (strain gauges) are connected to the respective multi - pin sockets provided at control panel.

View of the Load cell balance (Wind tunnel) at Amrita Virtual Lab