Low speed wind tunnel

Aerodynamicists use wind tunnels to test models of proposed aircraft. In the tunnel, the engineer can carefully control the flow conditions which affect the forces on the aircraft. By making careful measurements of the forces on the model, the engineer can predict the forces on the full scale aircraft. And by using special diagnostic techniques, the engineer can better understand and improve the performance of the aircraft.

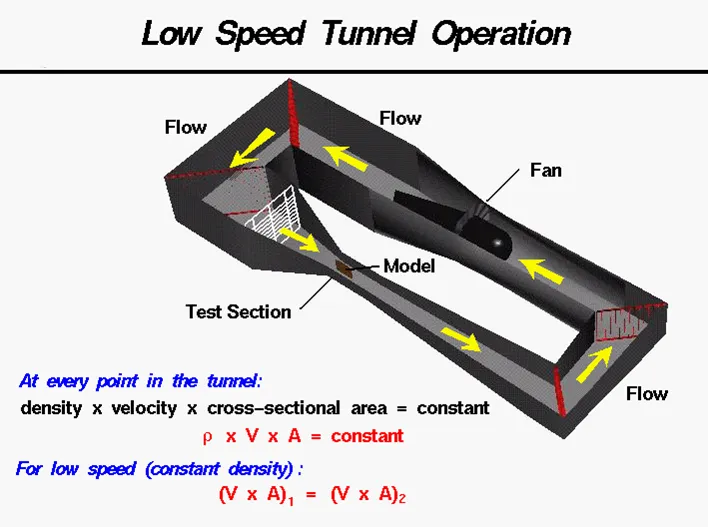
Wind tunnels are designed for a specific purpose and speed range and there is a wide variety of wind tunnel types and model instrumentation. The tunnel shown in the figure is a low-speed, closed tunnel which we are viewing from above. The air inside the tunnel is made to move by the fan on the far side of the tunnel. Air continuously circulates through the wind tunnel, passing over the model that is mounted in the test section.

The amount of air in the tunnel is a constant, and we can use the conservation of mass to relate local speed in the tunnel to the cross-sectional area. At every point in the tunnel, the velocity V times the air density rho times the area A is a constant. (rho is a Greek letter commonly used to denote the air density.)

rho * V * A = constant

For a low speed tunnel the density remains constant through the tunnel and we can further simplify the equation. Between any two places in the tunnel:

( V * A)1 = (V * A)2

Decreasing the area increases the velocity in a subsonic wind tunnel. We want the highest velocity in the test section and that is why the test section of the tunnel is designed to have the smallest cross-section.

The model is instrumented to provide the engineer with test data. To obtain meaningful data, the engineer must insure that the flow similarity parameters of Mach number and Reynolds number match the desired flight conditions. Both the Mach number and the Reynolds number depend on the velocity and density in the tunnel.