Aerodynamic Lift, Drag and Moment Coefficients

In the previous post we introduced the four fundamental forces acting on an aircraft during flight: Lift, Drag, Thrust and Weight and examined how they interact with one-another. We are now going to look more closely at the two aerodynamic forces Lift and Drag. We will look at the relationship between the two forces, study how they interact with one another, and learn how to non-dimensionalize the resulting forces. Let’s do this!

Two of the four fundamental forces acting on an aircraft during flight come about as a result of the aerodynamic loading on the body as it flies through the air. If you have read the previous post you will understand that lift must be produced by the airplane wing in order to act as a counter-force to the total flying weight, and that as a natural consequence to the motion of the aircraft through the air, a drag force that opposes this motion is also present. In this post we will examine how and why aerodynamic forces are generated as the airplane moves through the air, and introduce a method to non-dimensionalize the forces such that aircraft of various shapes and sizes can be directly compared to one-another.

We are going to specifically focus on the wing for the rest of this tutorial but the concept behind aerodynamic loading can just as easily be extended to any other component of the aircraft such as the fuselage, an engine cowling or even a canopy.

Pressure and Shear Loading

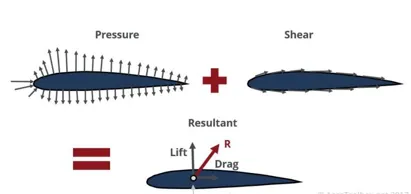
If you have ever stuck your hand out of a moving vehicle and felt the force of the air pushing on your hand you should intuitively have a pretty good idea of the concept of lift and drag. In this case the lift force tends to push your hand upward while the drag force pushes your hand backward. Here the force being exerted on your hand is being generated by two force distributions acting on your hand: a pressure distribution and a shear distribution.

Pressure (normal) and Shear (parallel) distribution on an airfoil

Exactly the same thing happens when we consider an airfoil subjected to a flow of air over its surface: a pressure and shear distribution are present acting over the entire airfoil surface.

Taking the local pressure contribution at each point along the surface and adding each contribution together (integration) results in a net pressure force acting on the airfoil. Similarly, adding the shear contribution along the airfoil surface results in a net shear force.

It is important to remember that the above result is true irrespective of the shape of the surface in question; the net aerodynamic force acting on any body in a free stream of air will always be the sum of the pressure and shear distributions acting along the body.

The net vertical force is termed the lifting force and the net horizontal force is termed the drag force. The net lift and drag force acts at the center of pressure of the airfoil. However, the center of pressure is not a fixed point and will vary as the angle of attack of the airfoil is varied.

The center of pressure is therefore not a convenient location about which to specify the resultant forces acting on the airfoil as it is not fixed. A common convention is to use a point specified at the airfoil quarter chord. This is a point located one quarter of the way along the chord from the leading edge. Moving the resultant lift and drag force from the center of pressure to the quarter chord requires that a moment be added to achieve a force balance. Thus a pitching moment equal to the lift force multiplied by the moment arm between the quarter chord and the center of pressure is added to achieve static equilibrium (Here we have neglected the component of the shear force that would contribute to the total pitching moment as it is negligibly small relative to the lift component).

We can therefore specify the resulting aerodynamic force on the airfoil as a lift and drag force acting at the quarter chord plus a balancing pitching moment.

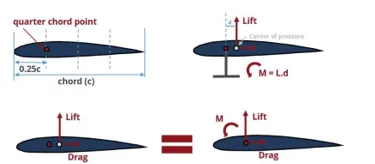
The location of the Quarter Chord and resolving the resultant aerodynamic force to components and a moment

Non-dimensional Coefficients

We have shown above that the aerodynamic properties of any body can be represented by resolving the resulting force into its normal (lift) and parallel (drag) components. We have also illustrated how it is often convenient to represent the resulting force on the body in terms of its force components and a moment about a fixed arbitrary point (the quarter chord in our example).

The answer lies in a clever use of mathematics, performing an exercise where the various forces are non-dimensionalized.

Each aerodynamic force is a function of the following parameters:

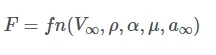
We can therefore non-dimensionalize the forces and moment in the following way:

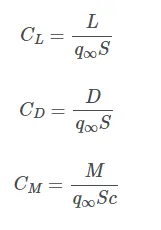
Where:

These non-dimensional representations of the lift, drag and pitching moment allow one to compare two aerodynamic bodies of different size, shape, and orientation to one another having normalised the result to account for the variation in the force produced by the size of the body and the conditions of flow.