Types of Control Engineering
Control engineering has its own categorization depending on the different methodologies used. The main types of control engineering include:
The systems are usually represented by using ordinary differential equations. In classical control engineering, these equations are transformed and analyzed in a transformed domain. Laplace transform, Fourier transform and z transform are examples. This method is commonly used in Single Input Single Output systems (SISO).
In modern control engineering, higher order differential equations are converted to first order differential equations. These equations are solved very similar to vector method. By doing so, many complications dealt in solving higher order differential equations are solved.
These are applied in Multiple Input Multiple Output systems where analysis in the frequency domain is not possible. Nonlinearities with multiple variables are solved by modern methodology. State space vectors, Eigenvalues, and Eigen Vectors belong to this category. State Variables describe the input, output and system variables.
In robust control methodology, the changes in the performance of the system with the change in parameters are measured for optimization. This aids in widening the stability and performance, also in finding alternate solutions. Hence in robust control, the environment, internal inaccuracies, noises, and disturbances are considered to reduce the fault in the system.
In optimal control engineering, the problem is formulated as a mathematical model of the process, physical constraints and performance constraints, to minimize the cost function. Thus optimal control engineering is the most feasible solution for designing a system with minimum cost.
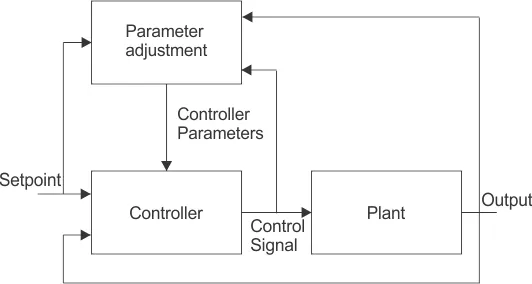
In adaptive control engineering, the controllers employed are adaptive controllers in which parameters are made adaptive by some mechanism. The block diagram given below shows an adaptive control system.

In this kind of controllers, an additional loop for parameter adjustment is present in addition to the normal feedback of process.
Nonlinear control engineering focuses on the nonlinearities which cannot be represented by using linear ordinary differential equations (i.e. they are not linear control systems). This system will exhibit multiple isolated equilibrium points, limit cycles, bifurcations with finite escape time. The main limitation is that it requires laborious mathematical analysis. In this analysis, the system is divided into the linear part and the nonlinear part.
In game theory, each system will have to reduce its cost function against the disturbances/noises. Hence it is a study of conflict and cooperation. The disturbances will try to maximize the cost function. This theory is related to robust and optimal control engineering.