Block Diagram Algebra

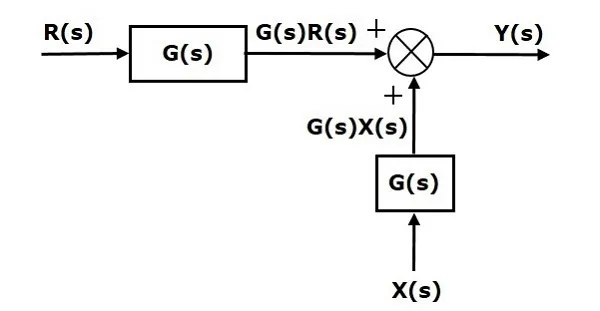
Similarly, you can represent parallel connection of ‘n’ blocks with a single block. The transfer function of this single block is the algebraic sum of the transfer functions of all those ‘n’ blocks.
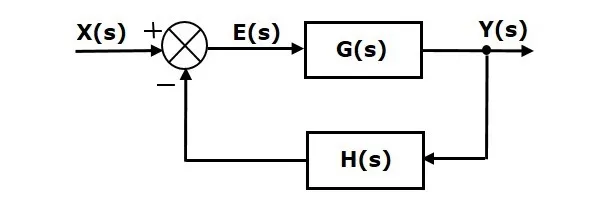
As we discussed in previous chapters, there are two types of feedback — positive feedback and negative feedback. The following figure shows negative feedback control system. Here, two blocks having transfer functions G(s)G(s) and H(s)H(s) form a closed loop.

The output of the summing point is -
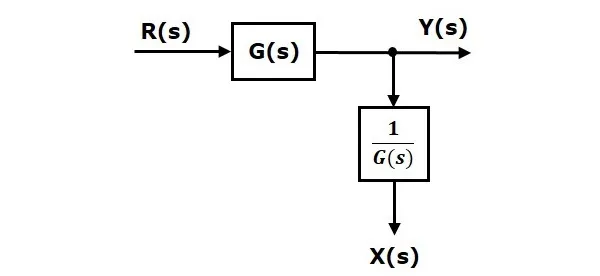

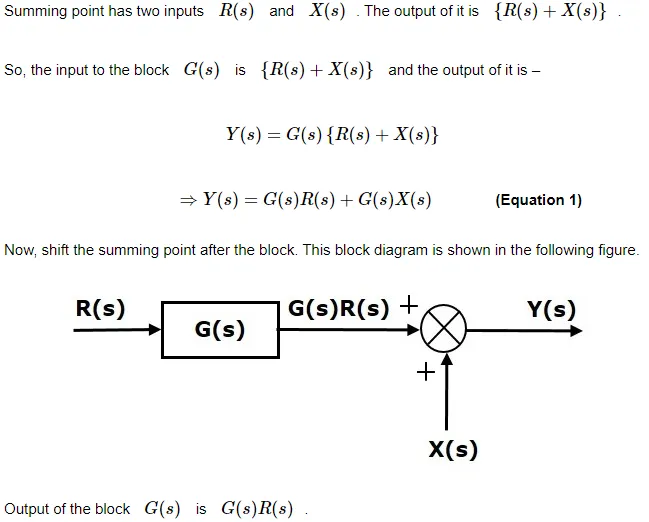


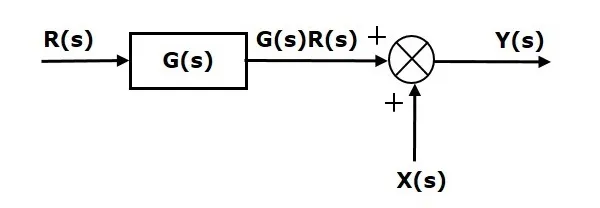
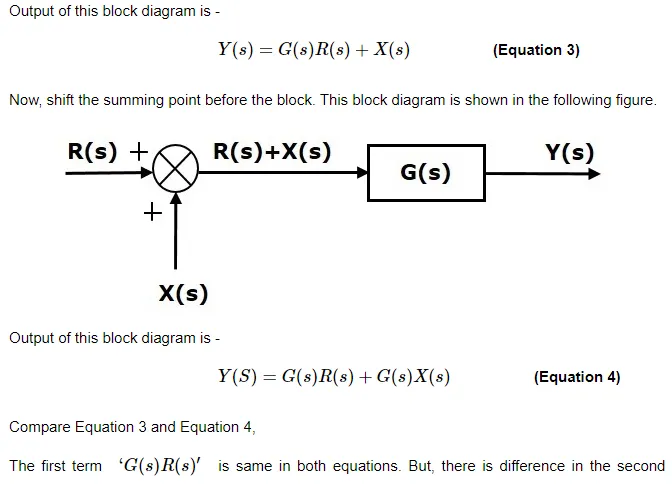
Consider the block diagram shown in the following figure. Here, the summing point is present after the block.

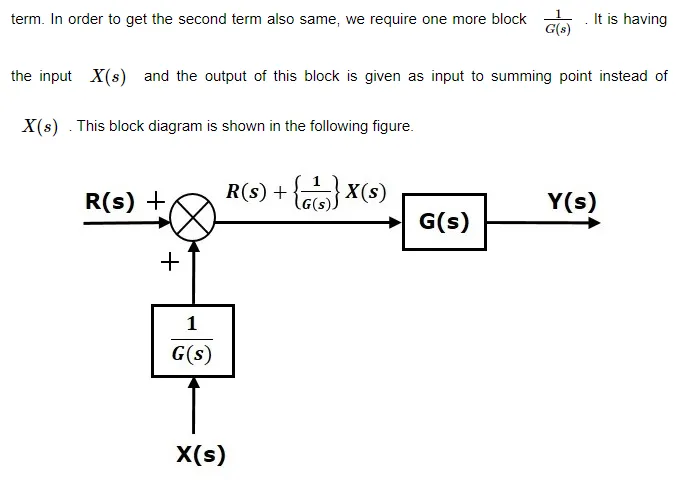
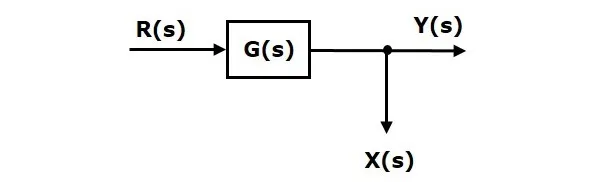
There are two possibilities of shifting the take-off points with respect to blocks −
Let us now see what kind of arrangements are to be done in the above two cases, one by one.
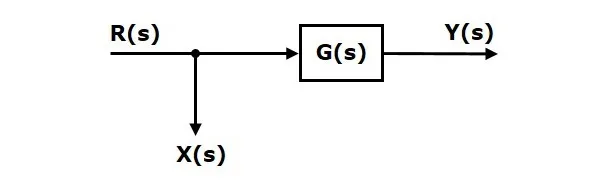
Consider the block diagram shown in the following figure. In this case, the take-off point is present before the block.



Consider the block diagram shown in the following figure. Here, the take-off point is present after the block.


