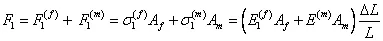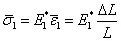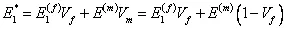The total axial force in the composite is sum of the axial forces in fibre and matrix. Thus, the total axial force in the composite substituting the expressions for axial strains in fibre and matrix from Equation (7.14) in above equation, can be given as
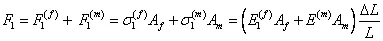
| (7.17) |
Now 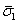 be the average axial stress in composite. The total cross sectional area of the composite is be the average axial stress in composite. The total cross sectional area of the composite is 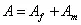 . Thus, using the average axial stress and cross sectional area of the composite, the axial force is . Thus, using the average axial stress and cross sectional area of the composite, the axial force is

| (7.18) |
Thus, combining Equation (7.17) and Equation (7.18) and rearranging, we get

| (7.19) |
Figure 7.3: (a) Undeformed unit cell under 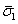 (b) and (c) deformed individual constituents of the unit cell (b) and (c) deformed individual constituents of the unit cell |
Let us define
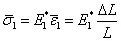
| (7.20) |
Further, noting that the ratios 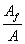 and and 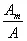 for same length of fibre and matrix represent the fibre and matrix volume fractions, respectively. Thus, combining Equations (7.19) and (7.20), we get for same length of fibre and matrix represent the fibre and matrix volume fractions, respectively. Thus, combining Equations (7.19) and (7.20), we get
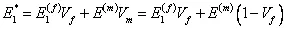
| (7.21) |
The above equation relates the axial modulus of the composite to the axial moduli of the fibre and matrix through their volume fractions. Thus, the effective axial modulus is a linear function of the fiber volume fraction. This equation is known as rule of mixtures equation. It should be noted that the effective properties are functions of the fiber volume fractions; hence it should always be quoted in reporting the effective properties of a composite. | 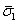
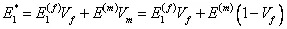
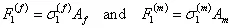
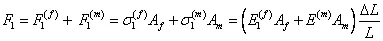
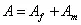 . Thus, using the average axial stress and cross sectional area of the composite, the axial force is
. Thus, using the average axial stress and cross sectional area of the composite, the axial force is