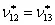 - axial Poisson’s ratio (for loading in
- axial Poisson’s ratio (for loading in 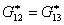 - axial shear modulus (shear stress parallel to the fibers)
- axial shear modulus (shear stress parallel to the fibers)Strength of Material Approximations:
In general, the laminates made are thin. Hence, for such laminates the analysis done using Kirchhoff and plane stress assumptions is reasonably good. For such analysis, one needs the engineering constants that occur in defining planar constitutive equations. These engineering constants are:
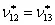 - axial Poisson’s ratio (for loading in
- axial Poisson’s ratio (for loading in 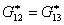 - axial shear modulus (shear stress parallel to the fibers)
- axial shear modulus (shear stress parallel to the fibers)Further, it is seen that for transversely isotropic composite, four out of five (the fifth one is ![]() ) properties can be developed from this approach. For the planar hygro-thermal analysis of such laminates, one can also obtain the in-plane coefficients of thermal expansions
) properties can be developed from this approach. For the planar hygro-thermal analysis of such laminates, one can also obtain the in-plane coefficients of thermal expansions ![]() and
and ![]() and hygroscopic expansion
and hygroscopic expansion ![]() and
and ![]() as well.
as well.
It is important to note that this approach involves assumptions which do not necessarily satisfy the requirements of an exact elasticity solution. In this approach the effective properties will be expressed in terms of the elastic properties and volume fractions of the fiber and matrix. The lamina is considered to be an alternate arrangement of fibres and matrix. The RVE chosen in these derivations is shown in Figure 7.2. The RVE here does not take into account the cross sectional arrangement of fibres and matrix, rather it represents volume of the material through the cross sectional area of fibre and matrix.
|
Figure 7.2: (a) Unidirectional lamina, (b) RVE for unidirectional composite for prediction of elastic properties |
Let, ![]() and
and ![]() represent fibre area and matrix area, respectively.
represent fibre area and matrix area, respectively. ![]() and
and ![]() represent fibre and matrix widths, respectively.
represent fibre and matrix widths, respectively. ![]() be the length of the RVE.
be the length of the RVE.