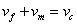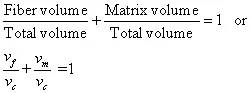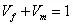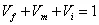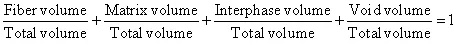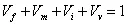Volume and Mass Fractions, Density and Void Content:
In the present section we are going to introduce some important concept of relative fraction of fibres and matrix by volume and mass. This is very important from the point that the most of the micromechanics based approaches use these fractions, along with the properties of individual phases, to express the properties of the equivalent homogeneous material.
In the present case, the effective properties of a composite are obtained with the assumption that the fibre is orthotropic or transversely isotropic and matrix is isotropic in behaviour. However, with appropriate changes, fibre can also be considered to be isotropic. In the following, the subscripts or superscripts ![]() and
and ![]() will denote fibre and matrix, respectively.
will denote fibre and matrix, respectively.
Volume Fractions:
As stated earlier, the fibre volume fraction is defined as the ratio of fibre volume to composite volume and matrix volume fraction is defined as the ratio of matrix volume fraction to composite volume. Let, ![]() be the volume occupied by fibres and matrix, respectively. Let,
be the volume occupied by fibres and matrix, respectively. Let, ![]() be the composite volume. We know that,
be the composite volume. We know that,
| (7.1) |
Thus, from these two definitions of volume fractions, we can write
| (7.2) |
Thus, in notations
| (7.3) |
where, ![]() denotes the fibre volume fraction and
denotes the fibre volume fraction and ![]() denotes the matrix volume fraction. Note that “total volume” and “composite volume” are used interchangeably.
denotes the matrix volume fraction. Note that “total volume” and “composite volume” are used interchangeably.
Note: If the interphase is also present as a third phase then, Equation (7.2) is modified as
|
|
or
| (7.4) |
where, ![]() denotes the interphase volume fraction and
denotes the interphase volume fraction and ![]() denotes the interphase volume.
denotes the interphase volume.
In case, there are voids present in composite, then the above equation becomes as
|
or
| (7.5) |
where, 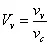 denotes the void volume fraction and
denotes the void volume fraction and ![]() denotes the void volume. In the remaining, we will consider that there are only two phases and Equation (7.3) is used.
denotes the void volume. In the remaining, we will consider that there are only two phases and Equation (7.3) is used.