Micromechanics

Strength of Materials Approach

Introduction

In the earlier lectures we have used the effective properties of the unidirectional layers in the development of various lamina or laminate mechanics issues. However, we know that at microscale the fibrous composites are heterogeneous. A composite is made of two main phases - fiber and matrix. Further, we know that apart from these two phases, additional phase may be present in the composite. These phases may be fillers, zones formed due to reaction between fibre and matrix and the coatings applied to the fiber, if any. The properties of these constituents, their amounts present and their distribution affect the effective properties of the composite.

It is now well understood that to determine the effective properties of a composite one needs to consider the microscale, that is, the scale at which the fibre and matrix are present. Thus, the study of composites at the fiber and matrix level is referred to as micromechanics.

In the present lecture we will present various methods to determine the effective hygro-thermo-mechanical properties of the composite. It is assumed that the properties of constituents, their arrangements and amounts are known a-priori.

 

 


Idealization of Microstructure of Fibrous Composite:

As mentioned earlier, the micromechanics is a study at fibre and matrix level. Thus, the geometry of arrangement of the fibres and matrix in a composite is an essential requirement to develop a model for the study. Some of the methods do not use the geometry of arrangement. Most of the methods developed for micromechanical analysis assume that:

  1. The fibers and matrix are perfectly bonded and there is no slip between them.
  2. The fibres are continuous and parallel.
  3. The fibres are assumed to be circular in cross section with a uniform diameter along its length.
  4. The space between the fibres is uniform throughout the composite.
  5. The elastic, thermal and hygral properties of fibre and matrix are known and uniform.
  6. The fibres and matrix obey Hooke’s law.
  7. The fibres and the matrix are only two phases in the composite.
  8. There are no voids in the composite.

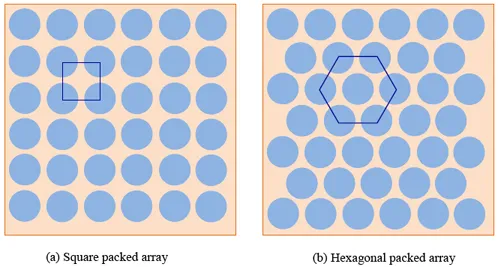
There are many ways to idealize the cross section of a lamina. In Figure 7.1 are shown two popular idealizations. The most commonly preferred arrangements are square packed and hexagonal packed arrays of fibres in matrix. The square and hexagonal packed arrays can be as shown in Figure 7.1(a), and (b), respectively.

In these idealizations it is seen that due to symmetry and periodicity of these arrays one can consider only one array to analyze the lamina at micro scale. Further, if this one array represents the general arrangement of fibres with respect to matrix and the interactions of fibre and matrix phases, then such array is called Representative Volume Element (RVE). Further, this RVE as a volume of material statistically represents a homogeneous material. In the analysis of an RVE the boundary conditions are chosen such that they reflect the periodicity. Thus, the arrays shown in Figure 7.1 are various RVEs. One should be able to see that the RVE also reflects the volume fractions. The term RVE was first coined by Hill in 1963.  
For example, the square RVE represents a lower fibre volume fraction than a hexagonal RVE. Note that RVE is also called as Unit Cell.

Figure 7.1: Idealization of cross section of a lamina